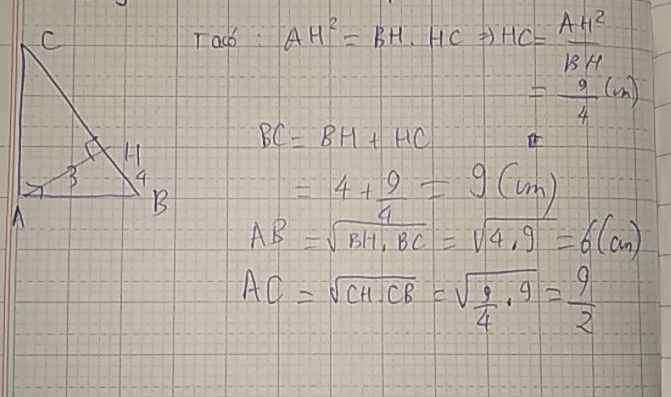Ta có:
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=\dfrac{9}{4}\left(cm\right)\)
\(BC=BH+HC=4+\dfrac{9}{4}=9\left(cm\right)\)
\(AB=\sqrt{BH.BC}=\sqrt{4.9}=6\left(cm\right)\)
\(AC=\sqrt{CH.BC}=\sqrt{\dfrac{9}{4}.9}=\dfrac{9}{2}\left(cm\right)\)
\(AH^2=BH.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích hai hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=2,25cm\)
\(BC=BH+HC=4+2,25=6,25cm\)
\(AB^2=BH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giwac hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow AB=\sqrt{BH.BC}=\sqrt{4.6,25}=5cm\)
\(AC=\sqrt{BC^2-AB^2}\) (Pitago)
\(\Rightarrow AC=\sqrt{6,25^2-5^2}=3,75cm\)