Question

Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh rằng DI // EK

Answer 1

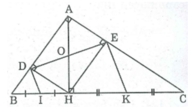
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH

⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)

⇒ ∆ IDB cân tại I ⇒ ∠ (DIB) = 180 0  - 2. ∠ B (1)

Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.

⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .

⇒  ∆ KHE cân tại K ⇒  ∠ (EKH) =  180 0 - 2. ∠ (KHE) (2)

Tứ giác ADHE là hình chữ nhật nên:

HE // AD hay HE // AB ⇒  ∠ B =  ∠ (KHE) (đồng vị)

Từ (1), (2) và (3) suy ra:  ∠ (DIB) =  ∠ (EKH)

Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).