Question

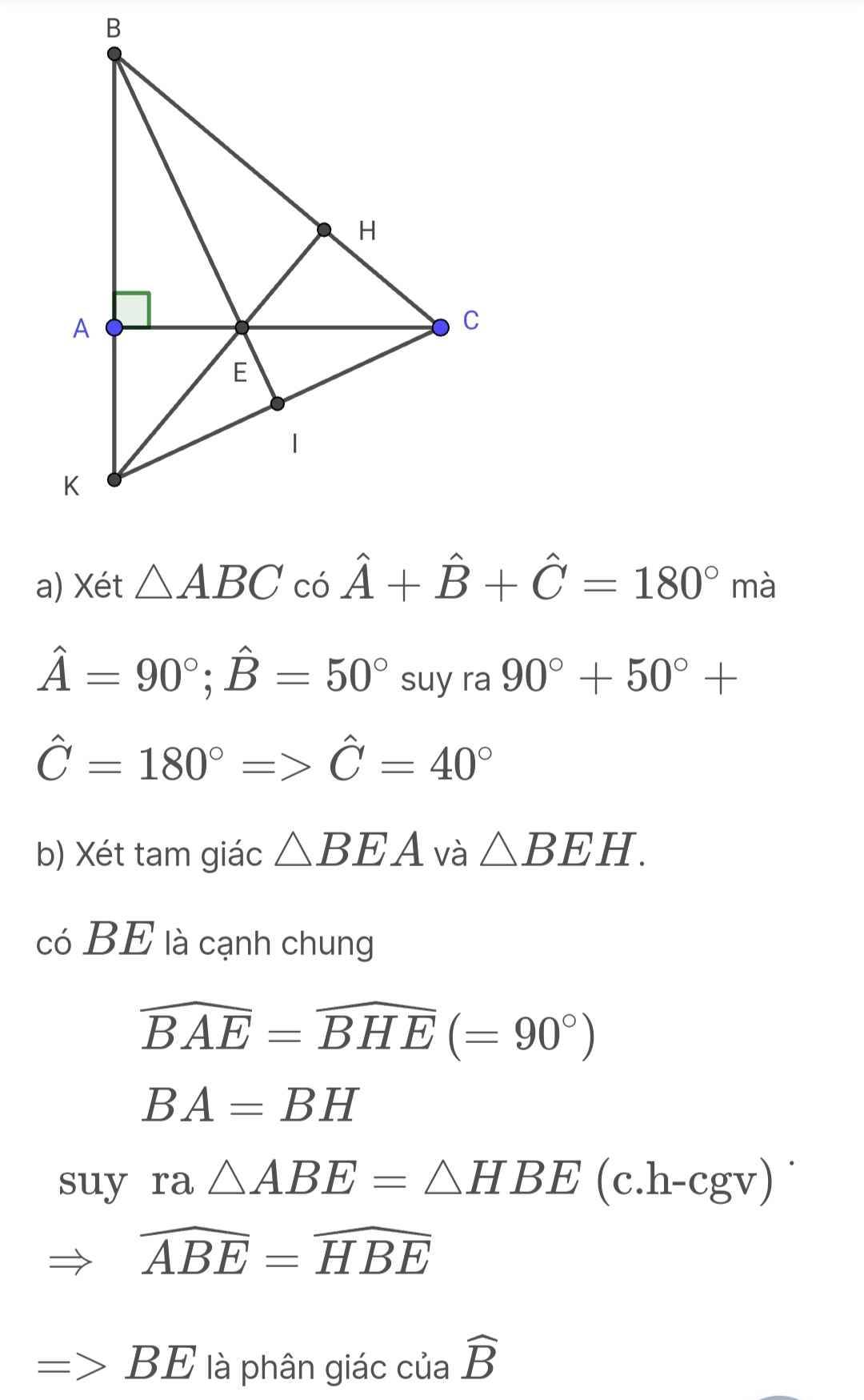
Cho tam giác $ABC$ vuông tại $A$ có $\hat{B}=50^{\prime \prime}$. Trên $BC$ lấy điểm $H$ sao cho $HB=BA$, từ $H$ kẻ $HE$ vuông góc với $BC$ tạ $H,(E$ thuộc $AC)$
a) Tính $\widehat{C}$.
b) Chứng minh $BE$ là tia phân giác góc $B$.
c) Gọi $K$ là giao điểm của $BA$ và $HE$, $BE$ cắt $KC$ tại $I$. Chứng minh rằng $I$ là trung điểm của $KC$.

Answer 1

a) xét tgABC có a ^ + B^ +c^ = 180 ddoooj mà A^=90 độ ; B^=50 độ suy ra 90 độ + 50 độ + C^ = 180 độ 

suy ra C^ = 40 độ

b ) xét tam giác BEA và tam giác BEH  có 

Be là cạnh chung

BAE^ =BHE^= 90 độ

suy ra  tam giác ABE = tam giác HBE ( ch - cgv )

suy ra BE là phân giác của B^

c) E là giao ddiemr của hai đường cao trong tam giác BKC nên BE vuông góc với KC 

tam giác BKC cân tại B có BI là đường cao nên BI là dduowmgf trung tuyến . do đó I là trung điểm của KC

Answer 2

a) Xét $△ABC$ có �^+�^+�^=180∘A^+B^+C^=180∘ mà �^=90∘;�^=50∘A^=90∘;B^=50∘ suy ra 90∘+50∘+�^=180∘=>�^=40∘90∘+50∘+C^=180∘=>C^=40∘
b) Xét tam giác $△BEA$ và $△BEH$.
có $BE$ là cạnh chung
 ���^=���^(=90∘)��=�� suy  ra △���=△��� (c.h-cgv) ⇒���^=���^  suy ⇒​BAE=BHE(=90∘)BA=BH ra △ABE=△HBE (c.h-cgv) ABE=HBE​.
$=>BE$ là phân giác của �^B
c) $E$ là giao điểm của hai đường cao trong tam giác $BKC$ nên $BE$ vuông góc với $KC$.

Tam giác $BKC$ cân tại $B$ có $BI$ là đường cao nên $BI$ là đường trung tuyến. Do đó $I$ là trung điểm của $KC$.

 

Answer 3

a) Xét $△ABC$ có �^+�^+�^=180∘A^+B^+C^=180∘ mà �^=90∘;�^=50∘A^=90∘;B^=50∘ suy ra 90∘+50∘+�^=180∘=>�^=40∘90∘+50∘+C^=180∘=>C^=40∘
b) Xét tam giác $△BEA$ và $△BEH$.
có $BE$ là cạnh chung
 ���^=���^(=90∘)��=�� suy  ra △���=△��� (c.h-cgv) ⇒���^=���^  suy ⇒​BAE=BHE(=90∘)BA=BH ra △ABE=△HBE (c.h-cgv) ABE=HBE​.
$=>BE$ là phân giác của �^B
c) $E$ là giao điểm của hai đường cao trong tam giác $BKC$ nên $BE$ vuông góc với $KC$.

Tam giác $BKC$ cân tại $B$ có $BI$ là đường cao nên $BI$ là đường trung tuyến. Do đó $I$ là trung điểm của $KC$.

Answer 4

f(a)+f(b)=f(a)+f(1−a)=100a+10100a​+1001−a+101001−a​=100a+10100a​+100a100​+10100a100​​=100a+10100a​+100a100​.100+10.100a100a​=100a+10100a​+10+100a10​=10+100a100a+10​=1(đpcm)

Answer 5

a) Góc C = 180 độ - (Góc A + Góc B)

=> Góc C = 180 độ - 90 độ - 50 độ

=> Góc C = 40 độ ( tổng 3 góc trong 1 tam giác bằng 180 độ )

b) Xét tam giác ABE và tam giác HBE có :

HB=BA ( theo đề bài )

Góc BAE= Góc BHE ( =90 độ )

Cạnh BE chung

=> Tam giác ABE = Tam giác BHE (c-g-c)

=> Góc ABE = Góc HBE 

=> BE là tia phân giác góc B 

c) Xét tam giác KBI và tam giác CBI , ta có : 

$E$ là giao điểm của hai đường cao trong tam giác $BKC$ nên $BE$ vuông góc với $KC$.

Tam giác $BKC$ cân tại $B$ có $BI$ là đường cao nên $BI$ là đường trung tuyến. Do đó $I$ là trung điểm của $KC$.

Answer 6

a) Xét $△ABC$ có �^+�^+�^=180∘A^+B^+C^=180∘ mà �^=90∘;�^=50∘A^=90∘;B^=50∘ suy ra 90∘+50∘+�^=180∘=>�^=40∘90∘+50∘+C^=180∘=>C^=40∘
b) Xét tam giác $△BEA$ và $△BEH$.
có $BE$ là cạnh chung
 ���^=���^(=90∘)��=�� suy  ra △���=△��� (c.h-cgv) ⇒���^=���^  suy ⇒​BAE=BHE(=90∘)BA=BH ra △ABE=△HBE (c.h-cgv) ABE=HBE​.
$=>BE$ là phân giác của �^B
c) $E$ là giao điểm của hai đường cao trong tam giác $BKC$ nên $BE$ vuông góc với $KC$.

Tam giác $BKC$ cân tại $B$ có $BI$ là đường cao nên $BI$ là đường trung tuyến. Do đó $I$ là trung điểm của $KC$.

Answer 7

a)Góc C=40 độ.

b)

Answer 8

too

Answer 9

a) Xét $△ABC$ có �^+�^+�^=180∘A^+B^+C^=180∘ mà �^=90∘;�^=50∘A^=90∘;B^=50∘ suy ra 90∘+50∘+�^=180∘=>�^=40∘90∘+50∘+C^=180∘=>C^=40∘
b) Xét tam giác $△BEA$ và $△BEH$.
có $BE$ là cạnh chung
 ���^=���^(=90∘)��=�� suy  ra △���=△��� (c.h-cgv) ⇒���^=���^  suy ⇒​BAE=BHE(=90∘)BA=BH ra △ABE=△HBE (c.h-cgv) ABE=HBE​.
$=>BE$ là phân giác của �^B
c) $E$ là giao điểm của hai đường cao trong tam giác $BKC$ nên $BE$ vuông góc với $KC$.

Tam giác $BKC$ cân tại $B$ có $BI$ là đường cao nên $BI$ là đường trung tuyến. Do đó $I$ là trung điểm của $KC$.

Answer 10

a)goc C= 180do-goc A- goc B= 180do-90do-50do=40do

suy ra goc C= 40do

 

Answer 11

a) góc C =A-B=180-50=40°

 

Answer 12

a) Xét tam giác EBH vuông tại H và tam giác EBA vuông tại A có

BH =BA (GT)

EB (CHUNG)

=> tam giác EBH = tam giác EBA( ch-cgv)

do đó góc HBE=gócABE( 2 góc t/ứ)

góc BEH = góc BEA( 2 góc t/ứ)

^BEH=180^o-^EBH-^EHB= 180^o-90^o- 50^o/2= 180^o-90^o-25^o=65^o

^HEC= 180^o-^AEH= 180^o- 2^BEH=180^o-2.65^o=50^o

Xét tam giác CEH có:

^ECH= 180^o-^HEC-^CHE= 180^o-50^o-90^o=40^o

Vậy ^C=40^o

^{b) Vì ^HBE=^ABE ( cmpa)}

^{Nên BE là tia p/g của^ABC (đpcm)}

^{c) Xét tam giác CKB} 

^{KH là đg cao của tam giác CKB}

^{CA là đg cao của tam giác CKB}

^{mà CA giao với KH tại E(gt)}

^{do đó E là trực tâm}

^{=> IB là đg cao của tam giác CBK}

Xét tam giác CIB và tam giác KIB có

IB là cạnh chung

^IBC=^IBK

=> tam giác cib= tam giác kib(ch-gn)

suy ra ic=ik( 2 cạnh t/ứ bn)

Vậy I là trung điểm của CK(đpcm).

Answer 13

a) Tam giác ABC có : góc A + góc B + góc C = 180 độ ( tổng 3 góc tam giác ) 

                                   90 độ + 50 độ + góc C = 180 độ 

                                           140 độ    + góc C = 180 độ 

                                                             góc C = 180 - 140 độ

                                                             góc C = 40 độ

b) Xét tam giác ABE vuông tại A và 

           tam giác HBE vuông tại H có : 

           AB = HB 

           BE cạnh chung 

=> tam giác BEA = tam giác BEH ( cạnh huyền - cạnh góc vuông ) 

=> góc ABE = góc HBE ( 2 góc tương ứng ) 

     Ta có : góc ABE = góc HBE = 1:2 góc ABH 

=> BE là tia phân giác góc ABH 

c) Ta có : BA vuông góc AC

                HE vuông góc BC

                BE và HE cắt nhau tại E 

=> BE vuông góc KC 

=> E là trực tâm 

=> BI là trung tuyến 

    Ta có : BI là trung tuyến 

                BE vuông góc KC

=> I là trung điểm KC

Answer 14

a, Ta có C=90°,B=40°

b,Ta có tam giác ABE=tam giác HBE(cạnh huyền-cạnh góc vuông)

Suy ra góc ABE=góc HBE(hai cạnh tương ứng)

Vậy BE là phân giác góc góc B

Answer 15

  

Answer 16

a, 40°

b,Xét tam giác ANE vuông tại A và tam giácHBE vuông tại h có:BE là cạnh chung/BH=BA/

=>Tam giác ABE=tam giác HBR(cạnh huyền-cạnh góc vuông)

--->góc HBE =góc ABE(2 góc tương ứng bằng nhau)

Vậy be là tia phân giác góc b 

c,Vì ei=2/3 bi nên bi là đường trung tuyến-->ik=ic Do đó i là trung điểm của kc

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Answer 17

Hjji

Answer 18

A )gốc c=90-50=40°

B) xét tam giác bae vuông tại a và tam giác bae vuông tại H có

Be chung

Ba=BH

∆bae=∆bhe

Góc Abe=góc hbe

Be là phân giác của góc ABC

C) xét∆bk có

Kh,ca là DG cao

Kh cắt ca tại e

E là trục tâm

Vậy be vuông góc KC

Answer 19

 

a) Vì tam giác ABC vuông tại A

=> Góc A=90*

=> Góc B+ góc C=90*

     50+C=90

           Vậy C=40*

b) Xét tam giác ANE vuông tại A và tam giác HBE vuông tại H có BE: cạnh chung

BH = BA

=> tam giác ABE bằng tam giác HBE (cạnh huyền - cạnh góc vuông )

Vậy góc HBE bằng góc ABE (hai góc tương ứng bằng nhau)

c) Vì góc ABE= góc HBE(cmt)

=>BE là tia phân giác của góc B

E là giao điểm của hai đường cao trong tam giác 

=> BE vuông góc KC

Tam giác BKC cân tại B có BI là đường cao

Nên BI là đường trung tuyến

Vậy I là trung điểm của KC(đpcm)

Answer 20

a,Xét tam giác ABC có:

Góc A+gócB+gócC=180*

Thay số:90*+50*+gócC=180*
                            GócC=180*-90*-50*=40*

 

Answer 21

a,Xét tam giác ABC có:

Góc A+gócB+gócC=180*

Thay số:90*+50*+gócC=180*
                            GócC=180*-90*-50*=40*

 

Answer 22

a,Xét tam giác ABC có:

Góc A+gócB+gócC=180*

Thay số:90*+50*+gócC=180*
                            GócC=180*-90*-50*=40*

 

Answer 23

a,Xét tam giác ABC có:

Góc A+gócB+gócC=180*

Thay số:90*+50*+gócC=180*
                            GócC=180*-90*-50*=40*

 

Answer 24

a,Xét tam giác ABC có:

Góc A+gócB+gócC=180*

Thay số:90*+50*+gócC=180*
                            GócC=180*-90*-50*=40*

 

Answer 25

a,Xét tam giác ABC có:

Góc A+gócB+gócC=180*

Thay số:90*+50*+gócC=180*
                            GócC=180*-90*-50*=40*

 

Answer 26

a,Xét tam giác ABC có:

Góc A+gócB+gócC=180*

Thay số:90*+50*+gócC=180*
                            GócC=180*-90*-50*=40*

 

Answer 27

gh

Answer 28