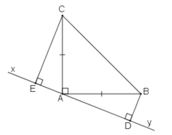
Ta có: ∠(BAD) +∠(BAC) +∠(CAE) =180o(kề bù)
Mà ∠(BAC) =90o (gt) ⇒∠(BAD) +∠(CAE) =90o (1)
Trong ΔAEC, ta có: ∠(AEC) =90o ⇒∠(CAE) +∠(ACE) =90o (2)
Từ (1) và (2) suy ra: ∠(BAD) =∠(ACE)
Xét hai tam giác vuông AEC và BDA, ta có:
∠(AEC) = ∠(ADB) = 90o
AC = AB (gt)
∠(ACE) = ∠(BAD) (chứng minh trên)
Suy ra: ΔAEC= ΔBDA (cạnh huyền- góc nhọn)








