Theo chứng minh trên, ta có:
DM = MH = 1/2 BH = 1/2.4 = 2(cm)
EN = NH = 1/2 CH = 1/2.9 = 4,5(cm)
DE = AH = 6(cm)
DENM là hình thang vuông, do đó diện tích của nó là:
S D E N M = 1/2(DM + EN)DE = 1/2.(2+4,5).6 = 19,5( c m 2 ).
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
Tính độ dài DE
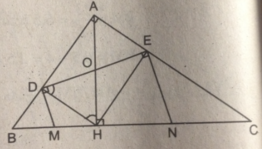
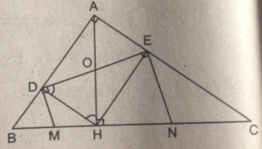
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N . Chứng minh M là trung điểm của BH , N là trung điểm của CH.
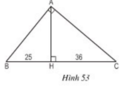
Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn thẳng có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó (h.53).
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành hai đoạn thẳng có độ dài 4cm và 9cm. Diện tích tam giác vuông đó là:
A. 39 c m 2
B. 36 c m 2
C. 18 c m 2
D. 27 c m 2
Cho tam giác vuông ABC vuông tại A, chân đường cao AH của tam giác ABC chia cạnh huyền BC thành hai đoạn thẳng BH = 4cm, HC = 9cm. Tính diện tích tam giác ABC?
A. S A B C = 39 c m 2
B. S A B C = 36 c m 2
C. S A B C = 78 c m 2
D. S A B C = 19 c m 2
Cho tam giác ABC vuông tại A có AH là đường cao. Từ H vẽ HD vuông góc với cạnh AB tại D, vẽ hE vuông góc với cạnh AC tại E. Biết AB = 15cm, BC = 25cm.
1)Tính độ dài cạnh AC và diện tích tam giác ABC.
2)Chứng minh tứ giác ADHE là hình chữ nhật.
3)Trên tia đối của AC lấy điểm F sao cho AF = AE. Chứng minh tứ giác AFDH là hình bình hành.
4)Gọi K là điểm đối xứng của B qua A, gọi M là trung điểm của AH. Chứng minh CM vuông góc HK.
Câu 1: Cho tam giác ABC vuông tại A ,đường cao AH
a) Cho biết HB=9cm,HC=16cm.Tính các độ dài AH,AB=AC
b) Chứng minh các hệ thức AH2=HB.HC,AB2=BC.BH
Câu 2: Tam giác ABC vuông tại A, đường cao AH, HB=4cm,HC=9cm.Gọi M là trung điểm của BC. Tính các cạnh của tam giác AHM .
Câu3: Cho tam giác ABC vuông tại A . Hình vuông MNPQ có M thuộc cạnh AB,N thuộc cạnh AC ,P và Q thuộc cạnh BC . Biết BQ=4cm,CP=9cm. Tính cạnh của hình vuông.
Câu 4: Tam giác ABC đường cao AH (H thuộc cạnh BC) có AH=6cm,BH=4cm,HC=9cm. Chứng minh rằng:
a) Tam giác AHB đồng dạng với tam giác CHA .
b) BAC = 90o
Câu 5: Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng : AE.AB=AD.AC
Câu 6: Cho hình thang ABCD (AB//CD) , M là trung điểm của AD,H là hình chiếu của M ten BC. Chứng minh rằng:Diện tích hình thang bằng tích BC.MH bằng cách vẽ đường cao BK, gọi N là trung điểm của BC và tìm các tam giác đồng dạng
Câu 7: Cho tam giác nhọn ABC , các đường cao BD và CE cắt nhau ở H . Gọi K là hình chiếu của H trên BC . Chứng minh rằng :
a) BH.BD=BK.BC
b) CH.CE=CK.CB
c) BH.BD+CH.CE=BC2
Câu 8: Cho hình bình hành ABCD (A<B) . Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD, H là hình chiếu của B trên AC. Chứng minh rằng :
a) AB.AE=AC.HC
b) BC. AK=AC.HC
c) AB.AE+AD.AK=AC2
Cho tam giác ABC vuông tại A (AB < AC ) có AH là đường cao ( H thuộc BC ) Gọi D và E lần lượt là hình chiếu của H trên AB và AC a) CMR : Tứ giác AEHD là hình chữ nhật b) CMR : ABH đông dạn AHD C) cho AB=9 cm và Ac = 12 cm. Tinh BC và diện tích ADHC d) Gọi M là giao điểm BE và CD . CMR BD . CM = EC. BM
