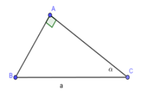
Cho tam giác ABC vuông tại A; BC = a không đổi, C ^ = α 0 0 < α < 90 0
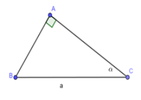
Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.
A. α = 45 0 ; m a x S A B C = 1 2 a 2 .
B. α = 30 0 ; m a x S A B C = 3 4 a 2 .
C. α = 60 0 ; m a x S A B C = 3 4 a 2 .
D. α = 45 0 ; m a x S A B C = 1 4 a 2 .
S A B C = . AB. AC ≤ 1 2 . A B 2 + A C 2 2 = 1 4 . A B 2 + A C 2
Áp dụng định lý Py-ta-go cho ABC vuông tại A ta có:
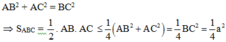
Dấu “=” xảy ra AC = AB => ∆ ABC vuông cân
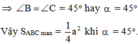
Đáp án cần chọn là: D