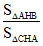Question

Cho tam giác ABC vuông tại A,  AB = 8cm, AC = 6cm, AD là tia phân giác góc A, D ∈ BC.

a) Tính DB/DC?

b) Kẻ đường cao AH (H ∈ BC). Chứng minh rằng: ΔAHB  ∼ Δ CHA

c) Tính  S AHB/ S CHA

 

Answer 1

a) Ta có: AD là tia phân giác của góc BAC

\(\Rightarrow\frac{AB}{AC}=\frac{DB}{DC}\)

\(\Leftrightarrow\frac{DB}{DC}=\frac{8}{6}\)

\(\Rightarrow\frac{DB}{DC}=\frac{4}{3}\)

b) Ta có: \(\widehat{B_1}+\widehat{C_1}=90^o\left(\Delta ABC\text{ vuông}\right)\)

              \(\widehat{C_1}+\widehat{HAC}=90^o\left(\Delta AHC\text{ vuông}\right)\)

         \(\Rightarrow\widehat{B_1}=\widehat{HAC}\left(=\widehat{C_1}\right)\)

Xét \(\Delta AHB\text{ và }\Delta CHA\)

Có: \(\widehat{AHC}=\widehat{AHB}\left(=90^o\right)\)

      \(\widehat{B_1}=\widehat{HAC}\)

\(\Rightarrow\Delta AHB~\Delta CHA\)

Answer 2

c) Xét tam giác ABC vuông tại A
<=> BC^2= AB^2+AC^2(áp dụng định lí Py-ta-go)
<=> BC^2= 100
<=> BC= 10   (cm)
Xét tam giác AHB ~ tam giác CHA (chứng minh trên)
<=> AH/CA= AB/CB
<=> AH= AB.CA /CB
<=> AH = 8.6 : 10 =  4,8 (cm)
Xét tam giác AHB vuông tại H
=> BH^2= AB^2-AH^2= 8^2-4,8^2=40,96
=> BH= 6,4 cm
Xét tam giác CHA vuông tại H
​=> CH^2=AC^2-AH^2=6^2-4,8^2=12,96
=> CH = 3,6 cm
Ta có:
S.AHB / S.CHA = (1/2 . BH.HA )/ (1/2 . HC .AH)
= BH / HC = 6,4 / 3,6 =16/9