Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 36 + 64 = 100 (cm)
Suy ra: BC = 100 = 10 (cm)
Ta có: sinC = AB/BC = 6/10 = 0,6
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
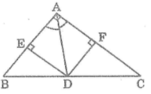
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
b) Phân giác của góc A cắt BC tại D. Tính BD, CD
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm. Phân giác của góc A cắt BC ở D. Tính BD, CD
: Cho tam giác ABC vuông tại A, AC= 8cm, AB = 6cm, BC = 10cm, đường cao AH
a. C/m tam giác ABC vuông tại A
b. Tính AH, BH, CH, góc C, góc B.
c. Trên BC lấy điểm M. Gọi hình chiếu của M trên AB, AC lần lượt là P, Q.
+ C/m PQ = AM.
+ Hỏi M ở vị trí nào thì PQ nhỏ nhất?
Tam giác ABC vuông tại A,có AB=6cm,AC=8cm a) Tính BC,góc B, góc C b)Phân giác của góc A cắt BC tại D.TínhBD,CD C) từ D kẻ DE và DF lần lượt vuông góc với AB,AC.Tứ giác AEDF là hình gì? Tính chu vui và diện tích của tứ giác AEDF
Cho tam giác ABC có AB=6cm AC=8cm BC=10cm
a) cm tam giác ABC vuông tại A
b) Tính góc B góc C và đường cao AH của tam giác ABC
c) Tính bán kính r của đường tròn (O) nội tiếp tam giác ABC
Cho tam giác ABC có AB=6cm AC=8cm BC=10cm
A chứng minh tam giác ABC vuông
B ;từ A hạ AH vuông góc với BC (H€BC) . Gọi M, N lần lượt là hình chiếu của H trên AB và AC. Tính BH và MN
C,Tính diện tích tứ giác MHNA
D,chứng minh góc AMN bằng góc ACB
BÀI 1 : Gọi AM, BN, CL là ba đường cao của tam giác ABC .Chứng minh
a) tam giác ANL đồng dạng tam giác ABC
b) AN.BL.CM=AB.BC.CA.cosA.cosB.cosC
BÀI 2: Cho tam giác ABC vuông tại A , AB=6cm, AC=8cm
a) Tính BC, góc B, góc C
b) phân giác của góc A cắt BC tại D .Tính BD,CD
cho tam giác ABC có AB=6cm , AB=8cm , BC=10cm ; đường cao AH gọi D,E thứ tự là hình chiếu của H trên AB và AC . Chúng minh : tam ABC vuông tại A . Tính góc B , góc C ? . Chứng minh tam giác ADE đồng dạng tam giác ACB
cho tam giác abc vuông tại a có ah là đường cao tính bc,ch abc (góc làm tròn đến độ ) với ab=6cm ab=8cm vẽ h vuông góc với ab e thuộc ab hf vuông góc với ac f thuộc ac chứng minh ae nhân ab bằng af nhân ac từ đó suy ra tam giác aef ~ tam giác acb gọi k là trung điểm của bc chứng minh ak vuông góc với ef