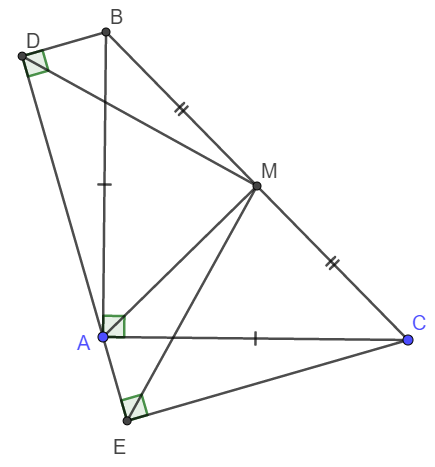
a) Ta thấy do tam giác ABD vuông nên \(\widehat{DBA}+\widehat{DAB}=90^o\)
Lại có \(\widehat{EAC}+\widehat{DAB}+\widehat{BAC}=180^o\Rightarrow\widehat{EAC}+\widehat{DAB}=90^o\)
Suy ra \(\widehat{DBA}=\widehat{EAC}\)
Xét tam giác vuông DBA và tam giác vuông EAC có:
BA = AC (Do ABC là tam giác cân tại A)
\(\widehat{DBA}=\widehat{EAC}\) (cmt)
\(\Rightarrow\Delta DBA=\Delta EAC\) (Cạnh huyền góc nhọn)
b) Do tam giác ABC vuông cân tại A nên \(\widehat{ABC}=45^o\) và trung tuyến AM đồng thời là đường cao.
Xét tam giác vuông AMB có \(\widehat{ABM}=45^o\) nên nó là tam giác vuông cân. Hay MB = MA.
c) Ta có AM là trung tuyến của tam giác cân nên đồng thời là phân giác.
Vậy thì \(\widehat{MAC}=45^o\)
\(\Rightarrow\widehat{DBM}=\widehat{DBA}+\widehat{ABM}=\widehat{EAC}+\widehat{CAM}=\widehat{EAM}\)
Do \(\Delta DBA=\Delta EAC\Rightarrow DB=EA\)
Suy ra \(\Delta DBM=\Delta EAM\left(c-g-c\right)\Rightarrow\widehat{BMD}=\widehat{AME};MD=ME\)
Từ đó ta có: \(\widehat{DME}=\widehat{DMA}+\widehat{AME}=\widehat{DMA}+\widehat{BMD}=\widehat{BMA}=90^o\)
Vậy nên tam giác DME vuông cân tại M.
22 tháng 1 2019 lúc 12:58












