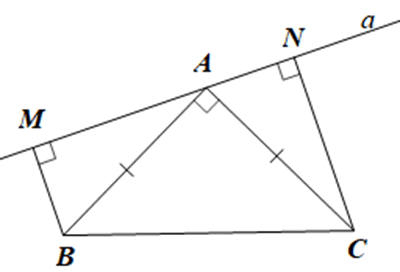
Lời giải:
a) Xét ∆MAB vuông tại M có: ˆABM+ˆMAB=90°���^+���^=90° (trong tam giác vuông, tổng hai góc nhọn bằng 90o).
Ta có ˆMAB+ˆBAC+ˆCAN=180°���^+���^+���^=180°
Suy ra ˆMAB+ˆCAN=180°−ˆBAC=90°���^+���^=180°−���^=90°
Lại có ˆABM+ˆMAB=90°���^+���^=90°
Suy ra ˆABM=ˆCAN���^=���^.
Vậy ˆABM=ˆCAN���^=���^.
b) Xét ∆MAB và ∆NCA có:
ˆBMA=ˆANC(=90°)���^=���^=90°,
BA = AC (vì tam giác ABC vuông cân tại A),
ˆABM=ˆCAN���^=���^ (chứng minh câu a).
Do đó ∆MAB = ∆NCA (cạnh huyền – góc nhọn).
Suy ra MA = NC (hai cạnh tương ứng).
Vậy MA = NC.
c) Vì tam giác ABC cân tại A nên ˆACB=ˆABC���^=���^
Lại có ˆACB+ˆABC+ˆBAC=180°���^+���^+���^=180° (tổng ba góc của tam giác ABC)
Suy ra ˆACB=ˆABC=180°−90°2=45°���^=���^=180°−90°2=45°.
• Nếu a // BC thì ˆMAB=ˆABC���^=���^ (hai góc so le trong).
Do đó ˆMAB=45°���^=45°.
Xét ∆ABM có ˆAMB+ˆMBA+ˆMAB=180°���^+���^+���^=180° (tổng ba góc của một tam giác)
Suy ra ˆMBA=180°−ˆAMB−ˆMAB=180°−90°−45°=45°���^=180°−���^−���^=180°−90°−45°=45°.
Do đó ˆMAB=ˆMBA���^=���^ (cùng bằng 45°).
Xét ∆AMB có ˆAMB=90°���^=90° và ˆMAB=ˆMBA���^=���^ nên ∆AMB vuông cân tại M.
Suy ra MA = MB (1)
• Nếu a // BC thì ˆCAN=ˆACB=45°���^=���^=45° (hai góc so le trong)
Xét ∆ABM có ˆACN+ˆANC+ˆCAN=180°���^+���^+���^=180° (tổng ba góc của một tam giác)
Suy ra ˆACN=180°−ˆANC−ˆCAN=180°−90°−45°=45°���^=180°−���^−���^=180°−90°−45°=45°.
Do đó ˆACN=ˆCAN���^=���^ (cùng bằng 45°).
Xét ∆ANC có ˆANC=90°���^=90° và ˆACN=ˆCAN���^=���^ nên ∆ANC vuông cân tại N.
Suy ra CN = AN (2)
Từ (1) và (2) suy ra MA = AN.
Vậy MA = AN.