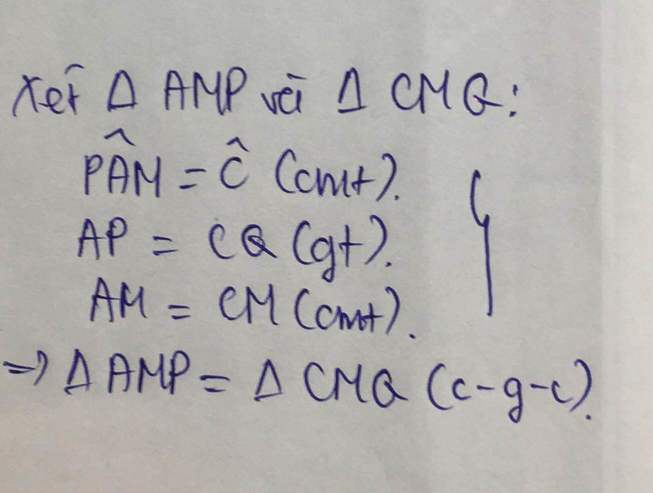Các câu hỏi tương tự
1.cho tam giác ABC có BC2AB. M là trung điểm của BC, D là trung điểm của BM.TRên tia AD lấy điểm E sao cho AE2AD. C/m: a, tam giác MAEtam giác MAC b, AC2AD2.cho tam giác ABC đều. D thuộc BC sao cho BC3BD.Vẽ DE vuông góc với BC(E thuộc AB) DF vuông góc với AC( F thuộc AC). C/m tam giác DEF đều.3. Cho tam giác ABC cân tại A.D thuộc AB. E thuộc AC sao cho ADAE. O là giao điểm của BE và CD. C/ma,BECD b, DE song song với BC
Đọc tiếp
1.cho tam giác ABC có BC=2AB. M là trung điểm của BC, D là trung điểm của BM.TRên tia AD lấy điểm E sao cho AE=2AD. C/m: a, tam giác MAE=tam giác MAC b, AC=2AD
2.cho tam giác ABC đều. D thuộc BC sao cho BC=3BD.Vẽ DE vuông góc với BC(E thuộc AB) DF vuông góc với AC( F thuộc AC). C/m tam giác DEF đều.
3. Cho tam giác ABC cân tại A.D thuộc AB. E thuộc AC sao cho AD=AE. O là giao điểm của BE và CD. C/m
a,BE=CD b, DE song song với BC
cho tam giác ABC nhọn . Trên cạnh BC lấy điểm M(M khác BC). Kẻ MH vuông góc AB (A thuộc AB),MK vuông góc AC (K thuộc AC). Trên tia đối của HM lấy điểm E sao cho HE=HM. Trên tia đối của KM lấy điểm F sao cho KF=KM. Gọi P ,Q lần lượt là các giao điểm của EF với AB và AC
a, CM tam giác AME cân
b, CM tam giác AEF cân
c, CM góc AMP= góc AMQ
1. Cho tam giác ABC vuông cân tại A. M là trung điểm của BC. Lấy điểm D bất kì thuộc BC.(D khác B , C , M). Gọi H và I là thứ tự chân đường vuông góc kẻ từ B , C xuống đường thảng AD. Đường thẳng AM cắt CI tại N. CMR :a) BH song song CIb) BH AIc) Tam giác HMI vuông cân2.Cho tam giác ABC có AB AC BC. M là trung điểm của BCa) CM : Tam giác AMB Tam giác AMCb) Trên tia đối của tia MA lấy điểm N sao cho M là trung điểm của AN. CM : Tam giác AMB Tam giác NMCc)Vẽ tia Ax vuông góc AM (AM thuộc nửa...
Đọc tiếp
1. Cho tam giác ABC vuông cân tại A. M là trung điểm của BC. Lấy điểm D bất kì thuộc BC.(D khác B , C , M). Gọi H và I là thứ tự chân đường vuông góc kẻ từ B , C xuống đường thảng AD. Đường thẳng AM cắt CI tại N. CMR :
a) BH song song CI
b) BH = AI
c) Tam giác HMI vuông cân
2.Cho tam giác ABC có AB = AC = BC. M là trung điểm của BC
a) CM : Tam giác AMB = Tam giác AMC
b) Trên tia đối của tia MA lấy điểm N sao cho M là trung điểm của AN. CM : Tam giác AMB = Tam giác NMC
c)Vẽ tia Ax vuông góc AM (AM thuộc nửa mặt phẳng bờ là đường thẳng AB chứa điểm C). Trên Ax lấy điểm P sao cho AP = AC. CM : P , N , C thẳng hàng.
3. Cho tam giác ABC vuông tại A , BD là tia phân giác của góc B ( D thuộc AC). Trên tia BC lấy điểm E sao cho BA = BE
a) CM : DE vuông góc BE
b) CM : BE là đường trung trực của AE.
c) Kẻ AH vuông góc BC. So sánh AH và EC
GIÚP MK VS NHA MN. BÀI HÌNH HỌC NÊN NHỜ MN VẼ HỘ MK CÁI HÌNH LUÔN NHA. mƠN MN NHÌU !!!!
cho tam giác ABC cân tại A ( góc A < 90 độ ). Kẻ BD vuông góc với AC ( D thuộc AC ), CE vuông góc với AB ( E thuộc AB ). BD cắt CE tại H.
a) cm tam giác ABD = tam giác ACE
b) CM tam giác BHC cân
c) Cm ED // BC
d) AH cắt BC tại K,trên tia HK lấy điểm M sao cho K là trung điểm của HM.Cm tam giác ACM vuông
Cho tam giác ABC cân tại A ( góc A < 90o ) . Kẻ BD vuông góc cới AC ( D thuộc AC ) , CE vuông góc với AB ( E thuộc AB ), BD và CE cắt nhau tại H
a) CM : Tam giác ABD = tam giác ACE
b) CM : Tam giác BHC cân
c) CM : ED // BC
d) AH cắt BC tại K , trên tia HK lấy điểm M sao cho K là trung điểm của HM . CM : tam giác ACM vuông
1, Cho tam giác ABC nhọn, trung tuyến AI. Trên nửa mặt phẳng bờ AC không chứa điểm B lấy điểm M sao cho tam giác ABM vuông cân tại A. Trên nửa mặt phẳng bờ Ab không chứa điểm C lấy điểm N sao cho tam giác ACN vuông cân tại A. Chứng minh rằng đường thẳng AI vuông góc với đường thẳng BC2, Cho tam giác ABC cân tại A, M thuộc cạnh BC sao cho MB MC. Lấy O thuộc đoạn thẳng AM. Chứng minh rằng widehat{AOB}widehat{AOC}
Đọc tiếp
1, Cho tam giác ABC nhọn, trung tuyến AI. Trên nửa mặt phẳng bờ AC không chứa điểm B lấy điểm M sao cho tam giác ABM vuông cân tại A. Trên nửa mặt phẳng bờ Ab không chứa điểm C lấy điểm N sao cho tam giác ACN vuông cân tại A. Chứng minh rằng đường thẳng AI vuông góc với đường thẳng BC
2, Cho tam giác ABC cân tại A, M thuộc cạnh BC sao cho MB < MC. Lấy O thuộc đoạn thẳng AM. Chứng minh rằng \(\widehat{AOB}>\widehat{AOC}\)
Cho tam giác ABC cân tại A (góc A < 90 độ). Kẻ BD vuông góc với AC (D thuộc AC), CE vuông góc với AB (E thuộc AB), BD và CE cắt nhau tại H
a) CM : Tam giác ABD = tam giác ACE
b) CM : Tam giác BHC cân
c) CM : ED // BC
d) AH cắt BC tại K, trên tia HK lấy điểm M sao cho K là trung điểm của HM. CM : tam giác ACM vuông
cho tam giác ABC cân tại A [góc A nhỏ hơn 90 độ ].Kẻ BD vuông góc AC [D thuộc AC ],CE vuông góc AB [E thuộc AB ],BD và CE cắt nhau tại H.
a] chứng minh tam giác ABD = tam giác ACE
b] Chứng minh tam giác BHC cân
c] chứng minh ED song song BC
d] AH cắt BC tại K, trên tia HK lấy điểm M sao cho K là trung điểm của HM. Chứng minh tam giác ACM vuông
cho tam giác ABC cân tại A,M là trung điểm của BC
1) c/m góc BAM = góc CAM
2) từ M kẻ MD vuông AB (D thuộc AB),kẻ ME vuông AC (E thuộc AC).c/m tam giác MDE là tam giác cân
3)c/m DE//BC
4)từ D kẻ DI vuông BC.Trên tia đối của tia ID lấy điểm K sao cho ID=IK.c/m ba điểm E,M,K thẳng hàng