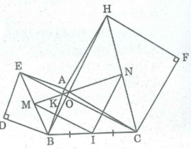
Ta có: ∠ (BAH) = ∠ (BAC) + ∠ (CAH) = ∠ (BAC) + 90 0
∠ (EAC) = ∠ (BAC) + ∠ (BAE) = ∠ (BAC) + 90 0
Suy ra: ∠ (BAH) = ∠ (EAC)
* Xét ∆ BAH và ∆ EAC , ta có:
BA = EA (vì ABDE là hình vuông)
∠ (BAH) = ∠ (EAC) (chứng minh trên)
AH = AC (vì ACFH là hình vuông)
Suy ra: ∆ BAH = ∆ EAC (c.g.c) ⇒ BH = EC
Gọi K và O lần lượt là giao điểm của EC với AB và BH.
Ta có: ∠ (AEC) = ∠ (ABH) (vì ∆ BAH = ∆ EAC) (1)
Hay ∠ (AEK) = ∠ (OBK)
* Trong ∆ AEK, ta có: ∠ (EAK) = 90 0
⇒ ∠ (AEK) + ∠ (AKE) = 90 0 (2)
Mà ∠ (AKE) = ∠ (OKB) (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra:
∠ (OKB) + ∠ (OBK) = 90 0
* Trong Δ BOK ta có:
∠ (BOK) + ∠ (OKB) + ∠ (OBK) = 180 0
⇒ ∠ (BOK) = 180 0 – ( ∠ (OKB) + ∠ (OBK) ) = 180 0 – 90 0 = 90 0
Suy ra: EC ⊥ BH












