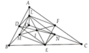
Gọi I trung điểm LE. Ta có DL//EN//OB và DL = EN = 0.5OB Þ DENL là hình bình hành. Tương tự chứng minh LMEF là hình bình hành. Từ đó suy ra EL,FM, DN đồng quy tại I
Cho tam giác ABC và điểm O nằm ở miền trong của tam giác. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC, CA. Gọi L, M, N lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh các đường thẳng EL, FM, DN cùng đi qua một điểm
cho tam giác AB.O là 1 điểm thuộc miền trong của tam giác.Gọi D,E,F lần lượt là trung điểm của các đoạn AB,BC,CA và I,M,N lần lượt là trung điểm của các đoạn OA,OB,OC.Chứng minh rằng EI,FM,DN đồng quy
cho tam giác abc và o là một điểm thuộc miền trong của tam giác gọi d,e,f lần lượt là trung ddiemr của các cạnh ab,bc,ca và l,m,n lần lượt là trung điểm của các đoạn oa, ob,oc
Cho tam giác ABC có:
O thuộc miền trong tam giác ABC
D;E;F lần lượt là trung điểm AB BC CA
L;M;N lần lượt là trung điểm OA OB OC
C/m EL;FM;DN đồng quy
Các bn giúp mk vs bài này khó quá
cho tam giác ABC và điểm O bất kỳ trong tam giác . Gọi L, M, N lần lượt là trung điểm cua OA, OB, OC và D, E, F lần lượt là trung điểm cua các cạnh AC, CB, BA. Chứng minh : các đường thẳng EL, FN, DM đồng quy
cho tam giác ABC và O là 1 điểm nằm ở miền trong tam giác. Gọi D, E, F, M, N, P lần lượt là trung điểm của AB, BC, CA, OA, OB, OC. CM : EM, FN, DP đồng quy
Cho tam giác nhọn ABC, O là trực tâm tam giác. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA.
Gọi R, S, T lần lượt là trung điểm của các đoạn OA, OB, OC.
a ) Tứ giác MPTS là hình gì ?
b ) Chứng minh 3 đường thẳng RN, MT, SP đồng quy.
Cho tam giác ABC và điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.
Bài 11: Cho tam giác nhọn ABC, O là trực tâm của tam giác. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA; R, S, T lần lượt là trung điểm của các đoạn OA, OB, OC
a) Tứ giác MPTS là hình gì? Vì sao?
b) Chứng minh ba đường thẳng RN,MT, SP đồng quy
c) Với điều kiện nào của tam giác ABC thif MR= RP= MS
