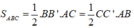Các câu hỏi tương tự
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C.
cho tam giác ABC biết AB=AC. Kẻ đường cao BH và CK.
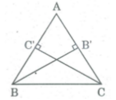
a) Viết công thức tính diện tích tam giác ABC theo độ dài đường cao BH VÀ CK.
b)tỉ số 2 đường chép xuất phát từ các đỉnh B cà C.
c)so sánh độ dài 2 đường cao BH VÀ CK.
Cho tam giác ABC, AB=3AC. Tính tỉ số đường cao xuất phát từ B và C
Cho tam giác ABC có AB=12 cm, AC=16cm. Hai đường cao xuất phát từ đỉnh B và C là BH và CK . Biết BH=9cm. Tính CK.
A. 12cm
B. 15cm
C. 9cm
D. 8cm
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C. Bài 2 Cho hình thang vuông ABCD (∠A = ∠D = 90°). Gọi H là điểm đối xứng với B qua AD, I là giao điểm của CH và AD. Chứng minh rằng ∠(AIB) = ∠(DIC)
tam giác ABC có G là trọng tâm và đường thẳng d không cắt cạnh nào của tam giác. Từ các đỉnh A,B,C và G kẻ các đường thẳng AA',BB',CC',GG' vuông góc với d. Chứng minh hệ thức: AA'+BB'+CC'=3GG'
Cho tam giác ABC. Đường thẳng xuất phát từ đỉnh A cắt BC tại K và cắt đường trung tuyến BM tại I sao cho \(\frac{BI}{IM}\)= \(\frac{1}{2}\). Tính tỉ số diện tích tam giác ABK và tam giác ABC .
Cho tam giác ABC có G là trọng tâm và một đường thẳng d không cắt cạnh nào của tam giác. Từ các đỉnh A,B,C và trọng tâm G ta kẻ các đoạn \(AA^,,BB^,,CC^,\)và \(GG^,\)vuông góc với đường thẳng d. Chứng minh hệ thức \(AA^,+BB^,+CC^,=3GG^,\)
cho tam giác ABC nhọn, các đường cao AA', BB', CC', H là trực tâm
a) tính tổng HA'/AA' + HB'/BB' + HC'/CC'
b) gọi AI là phân giác của tam giác ABC; IM, IN thứ tự là phân giác của góc AIC và góc AIB. Chứng minh rằng: AN.BI.CM = BN.IC.AM