O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
OD > OE ⇒ AB < AC
O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
OD > OE ⇒ AB < AC
Cho tam giác ABC, O là giao của các đường trung trực của tam giác; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, AC. Cho biết OD > OE, OE = OF (h.69).
Hãy so sánh các độ dài:
BC và AC;
Cho tam giác ABC, O là giao của các đường trung trực của tam giác; D, E, F theo thứ tự là trung điểm của các cạnh AB, BC, AC. Cho biết OD > OE, OE = OF (h.69).
Hãy so sánh các độ dài:
a) BC và AC;
b) AB và AC.
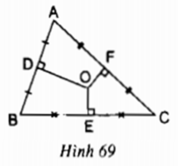
Cho tam giác ABC. D,E,F lần lượt là trung điểm của các cạnh AB, BC, AC và O là giao điểm các đường trung trực của tam giác ABC. Cho OD > OE; OE = OF. Hãy sao sánh BC và AC; AB và AC
Giúp mình bài này với
Cho tam giác ABC
a) Gọi M là trung điểm của AC. Biết BM = AC. Gọi D là điểm đối xứng của B qua A, gọi E là điểm đối xứng của M qua C. CMR: DM vuông góc với BE
b) Lấy điểm O bất kì trong tam giác. Các tia AO; BO; C cắt các cạnh BC; CA; AB thứ tự tại D; E; F. CMR:
b1) OD/AD + OE/BE + OF/CF = 1
b2) (1 + AD/OD)(1 + BE/OE)(1 + CF/OF) >= 64
Bài 1: Cho tam giác ABC (AC>AB) đường cao AH Gọi D E K theo thứ tự trung điểm của của AB AC BC. Chứng minh rằng
a. DE là trung trực của AH
b. DEKH là hình thang cân
Bài 2: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH, E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH=12 cm, BC=18 cm
Mn giải giúp mình bài này với ! Cho tam giác ABC nội tiếp đường tròn O biết góc A = 50 độ góc B = 70 độ. Gọi M, N, E theo thứ tự là trung điểm của AB, AC, BC. So sánh OM, ON, OE
Cho tam giác đều \(ABC\) có độ dài cạnh bằng \(a\). Gọi \(M\) là 1 điểm nằm trong tam giác. \(MI,MP,MQ\) theo thứ tự là khoảng cách từ \(M\) đến các cạnh \(BC,AB,AC\). Gọi \(O\) là trung điểm của cạnh \(BC\). Các điểm \(D\) và \(E\) theo thứ tự chuyển động trên các cạnh \(AB\) và \(AC\) sao cho \(\widehat{DOE}=60^o\).
\(a\)) Chứng minh: \(MI+MP+MQ\) không đổi.
\(b\)) Chứng minh: Đường thẳng \(DE\) luôn tiếp xúc với một đường tròn cố định.
\(c\)) Xác định vị trí của \(D\) và \(E\) để diện tích tam giác \(DOE\) đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó theo \(a\).
Cho tam giác ABC (AB nhở hơn AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại D,E.
a) Chứng minh nếu góc BAC bằng 45 độ thì AE=BE
b)Gọi H là giao điểm BE và CD. Chứng minh đường trung trực của đoạn DH đi qua trung điểm cảu đoạn AH
c)Chứng minh rằng đường thẳng OE là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
các bác giúp em câu c với
Cho tam giác ABC cân ở A. Gọi D, F lần lượt là trung điểm của AB, AC. Các đường trung trực của AB, AC cắt nhau tại O. Gọi G, E tương ứng là trọng tâm của tam giác ABC và ACD. Gọi H là trung điểm của BC. Từ G kẻ đường thẳng song song với AC cắt BC tại I. CM:
a) GH/AD = HI/DO
b) ADG đồng dạng với DOE
c) OE vuông góc với CD