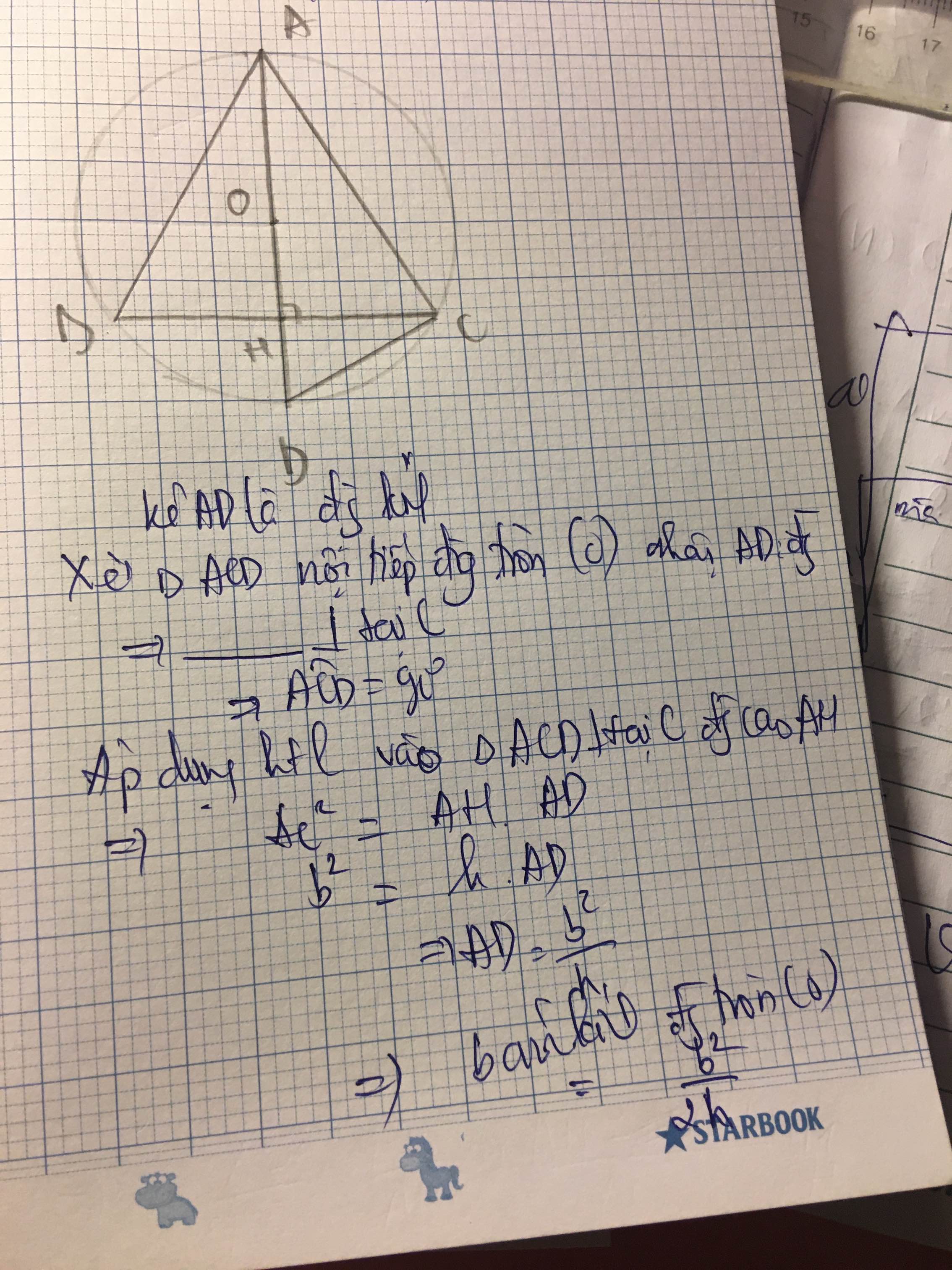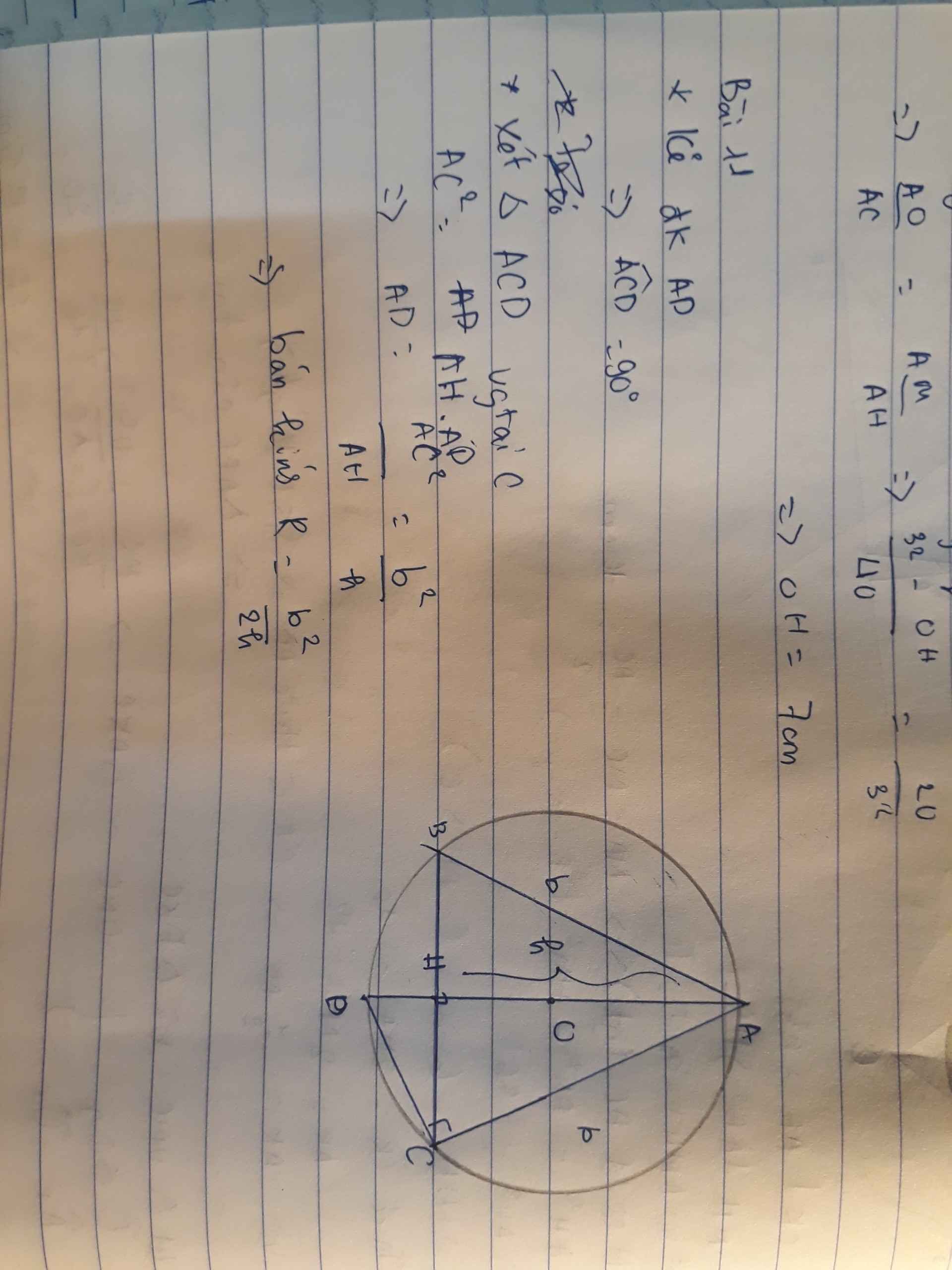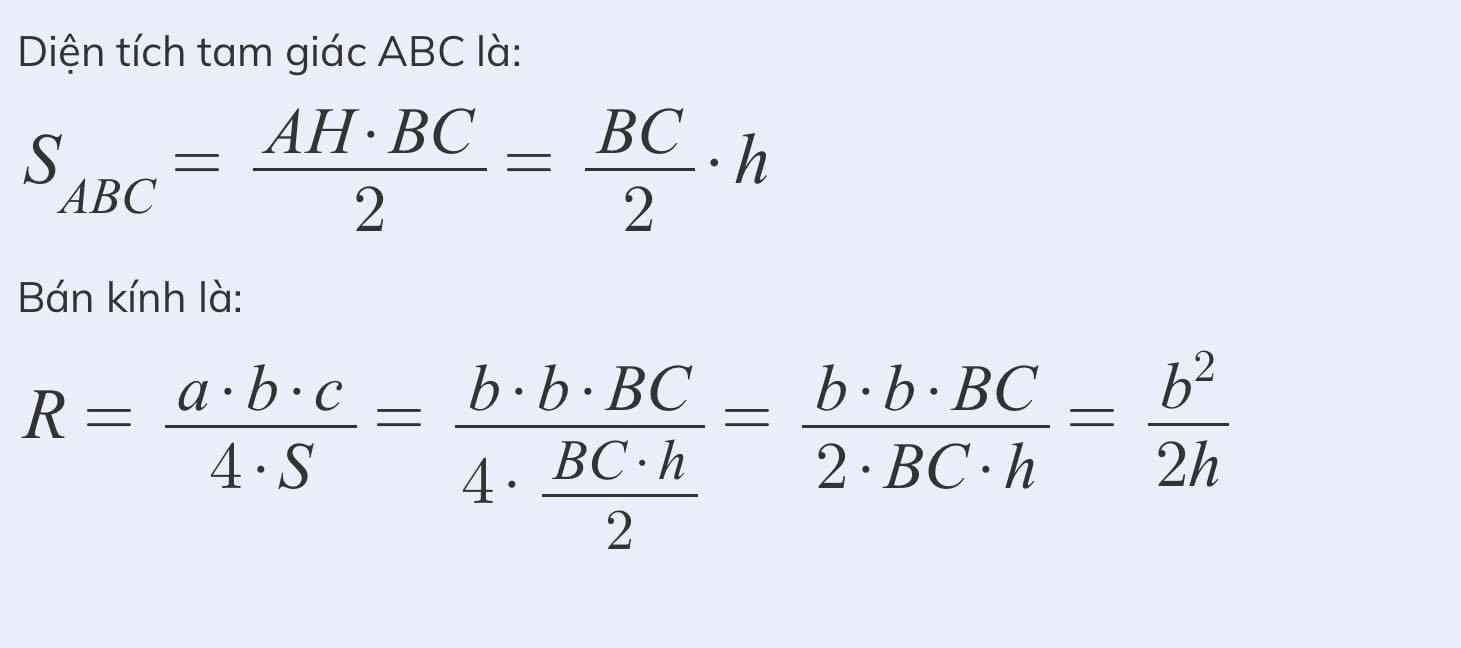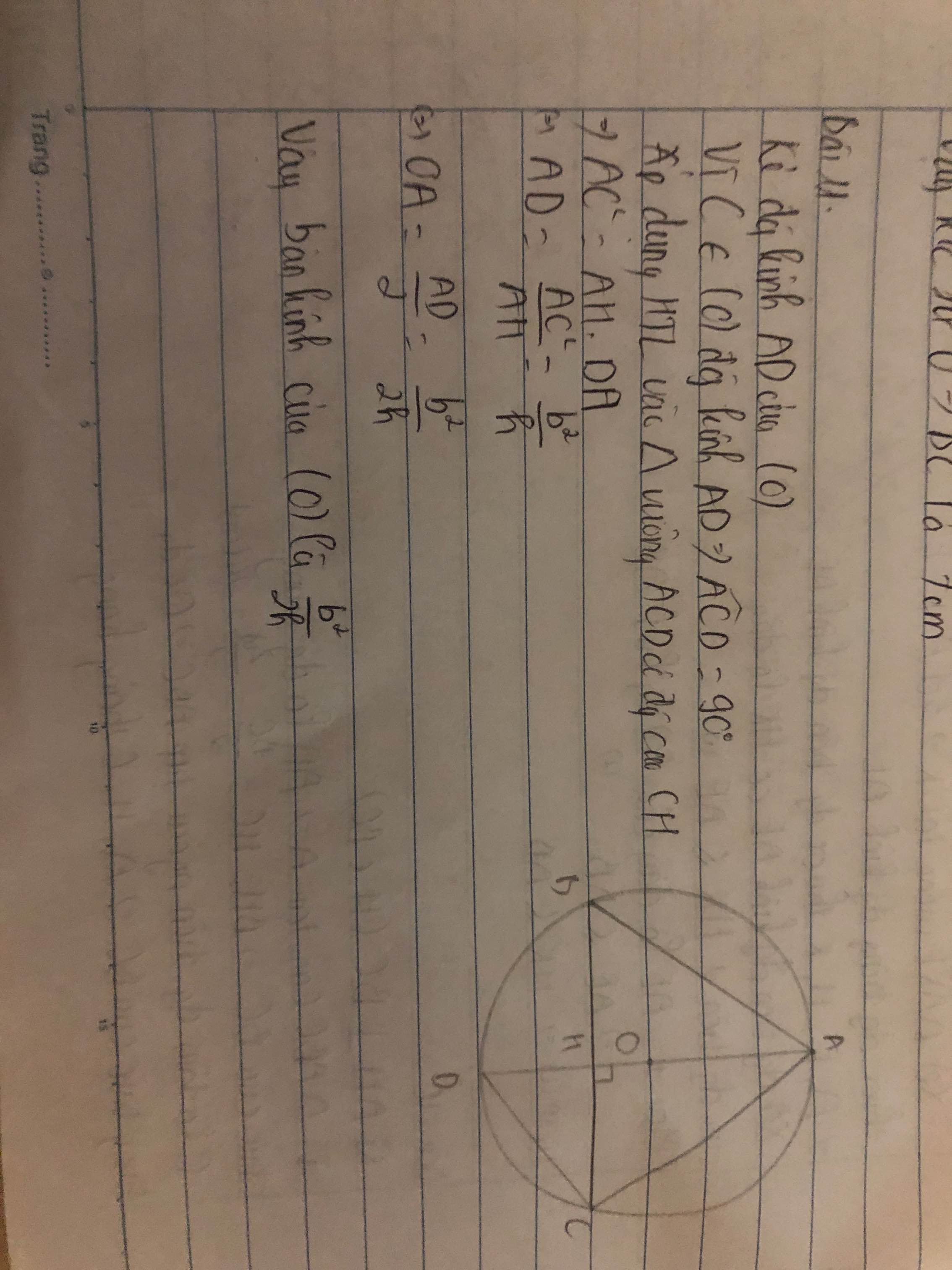Question

Cho tam giác ABC nội tiếp đường tròn (O ; R), cạnh bên bằng b, đường cao AH = h. Tính bán kính của đường tròn (O).

Answer 1

b²/2h

Answer 2

1

Answer 3

Ta có O là trọng tâm của tg ABC => AO là đường trung tuyến của tg ABC => AO là đường cao của tg ABC (Trong tg cân đường đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao và đường trung trực)

 

$\Rightarrow OH=\frac{AH}{3}=\frac{h}{3}$ (trong tg 3 đường trung tuyến cắt nhau tại 1 điểm gọi là trọng tâm của tg và cách đáy 1 khoảng = 1/3 chiều dài mỗi đường)

Xét tg vuông ABH có

$B{H}^2=A{B}^2+A{H}^2=b^2+h^2$

Xét tg vuông OBH có

$BO=R=\sqrt{B{H}^2+O{H}^2}=\sqrt{b^2-h^2+\frac{h^2}{9}}=\frac{1}{3}\sqrt{9b^2-8h^2}$

 

Answer 4

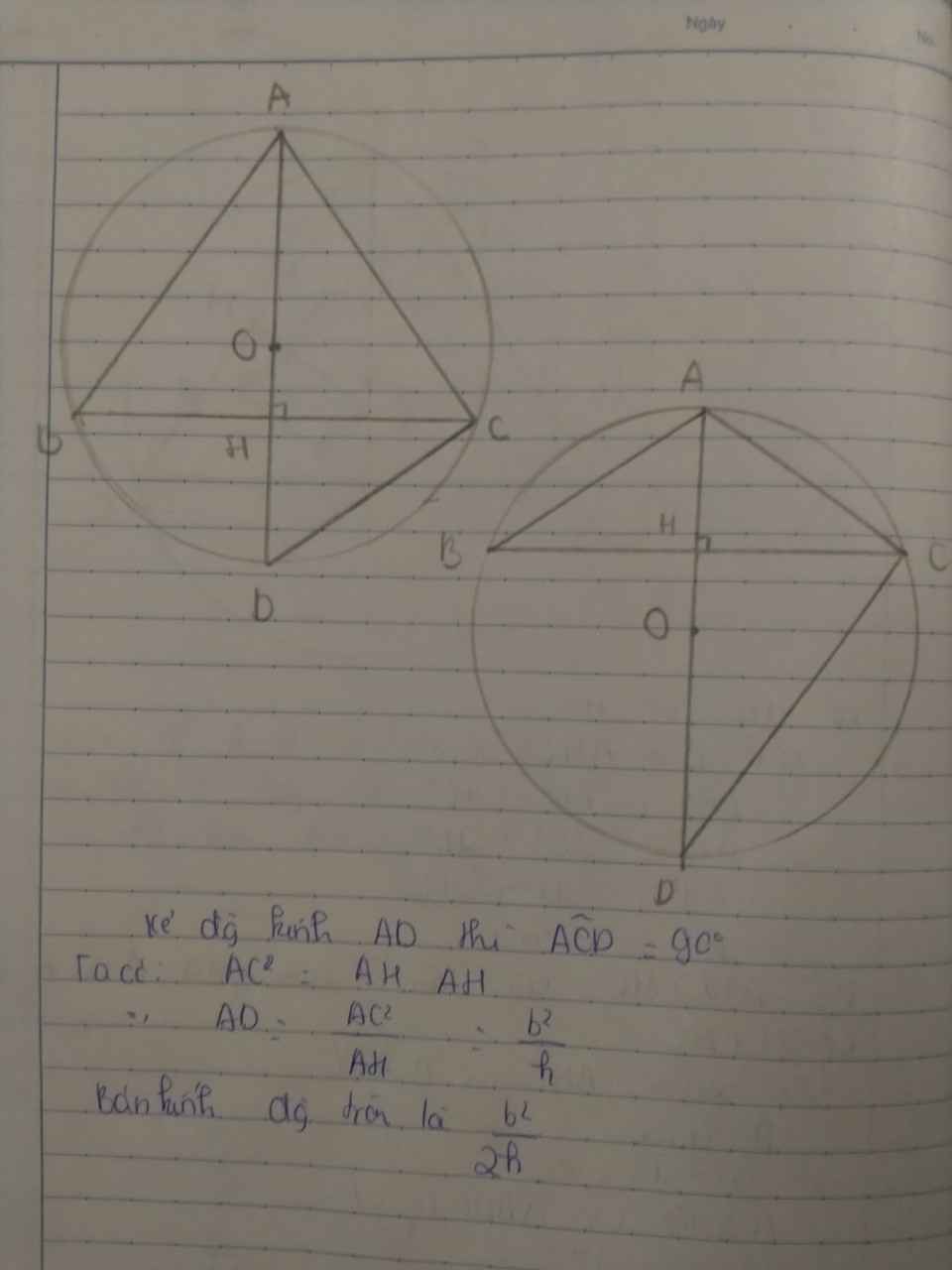
Kẻ đường kính AD thì \widehat{ACD}={90}^\circACD=90∘.

Ta có AC^2=AH.AHAC2=AH.AH nên AD=\frac{AC^2}{AH}=\frac{b^2}{h}AD=AHAC2​=hb2​. Bán kính đường tròn là \dfrac{b^2}{2h}2hb2​.

Answer 5

kẻ đường kính AD thì góc ACD =90độ 

ta có AC ^2=AH nhân AD nên AD=AC^2/AH=b^2/h

bán kính đường tròn là b^2/2h

Answer 6

Kẻ đường kính AD thì góc ACD=90 nên tam giác ACD vuông C

=>AC^2=AH.AD=>AD=AC^2/AH=b^2/h=>AO=b^2/2h\widehat{ACD}={90}^\circ

Answer 7

  

Answer 8

b^2/2h

Answer 9

b^2/2h

Answer 10

 

Answer 11

Answer 12

  

Answer 13

Kẻ đường kính AD thì \widehat{ACD}={90}^\circACD=90∘.

Ta có AC^2=AH.AHAC2=AH.AH nên AD=\frac{AC^2}{AH}=\frac{b^2}{h}AD=AHAC2​=hb2​. Bán kính đường tròn là \dfrac{b^2}{2h}2hb2​

Answer 14

Kẻ đường kính AD thì \widehat{ACD}={90}^\circACD=90∘.

Ta có AC^2=AH.AHAC2=AH.AH nên AD=\frac{AC^2}{AH}=\frac{b^2}{h}AD=AHAC2​=hb2​. Bán kính đường tròn là \dfrac{b^2}{2h}2hb2​.

Answer 15

bán kính đường tròn là b^2 / 2h

Answer 16

Kẻ đường kính AD thì \widehat{ACD}={90}^\circACD=90∘.

Ta có AC^2=AH.AHAC2=AH.AH nên AD=\frac{AC^2}{AH}=\frac{b^2}{h}AD=AHAC2​=hb2​. Bán kính đường tròn là \dfrac{b^2}{2h}2hb2​.

Answer 17

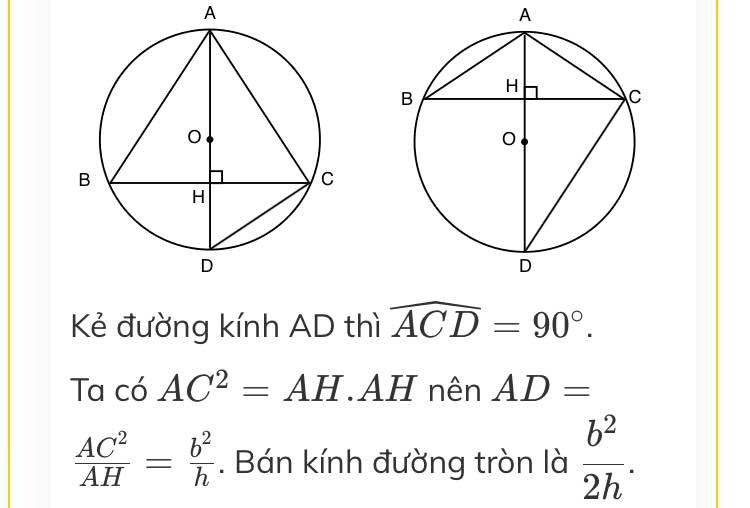
Kẻ đường kính AD thì góc ACD = \(90^0\)

Ta có \(AC^2\)= AD . AH nên 

AD =\(\dfrac{AC^2}{AH}=\dfrac{b^2}{h}\)

Bán kính của đường tròn bằng \(\dfrac{b^2}{2h}\)

Answer 18

Kẻ đường kính AD . Tam giác ACD nội tiếp đường tròn đường kính AD có tâm là trung điểm của AD =>  tam giác ACD vuông tại C => góc ACD = 90 độ . 
tạm giác ACD vuông tại C , đường cao CH . Áp đụng hệ thức giưax cạnh và đương cao trong tam giác vuông ta có :  AC^2=AH.AD => AD = \(\dfrac{AC^2}{AH}=\dfrac{b^2}{h}\)

Vậy bán kính đường tròn là \(\dfrac{b^2}{h}.\dfrac{1}{2}=\dfrac{b^2}{2h}\)

 

 

Answer 19

Kẻ đường kính AD thì \widehat{ACD}={90}^\circACD=90∘.

Ta có AC^2=AH.AHAC2=AH.AH nên AD=\frac{AC^2}{AH}=\frac{b^2}{h}AD=AHAC2​=hb2​. Bán kính đường tròn là \dfrac{b^2}{2h}2hb2​.

Answer 20

Kẻ đường kính AD thì ACD^=90∘ACD=90∘.ACD=90

Ta có AC=AH.AH nên AD =

b22h2hb2​.

   

Answer 21

kẻ đường kính AD .tam giấc ACD nội tiếp đường tròn đường kính AD có tâm là trung điẻm của AD=> tam giác ACD VUÔNG TỊ C =>ACD=90 ĐỌ TAM GIÁC ACD VUÔNG TẠI C

ĐƯỜNG CAO CH ,

Answer 22

Answer 23

 

Answer 24

Answer 25

Kẻ đường kính AD thì $\widehat{ACD}={90}^{\circ }$.

b22h.

Answer 26

ẻ đường kính AD thì \widehat{ACD}={90}^\circACD=90∘.

Ta có AC^2=AH.AHAC2=AH.AH nên AD=\frac{AC^2}{AH}=\frac{b^2}{h}AD=AHAC2​=hb2​. Bán kính đường tròn là \dfrac{b^2}{2h}2hb2​.

Answer 27

 

Answer 28

  

Answer 29

Answer 30

Kẻ đường kính AD thì \widehat{ACD}={90}^\circACD=90∘.

Ta có AC^2=AH.AHAC2=AH.AH nên AD=\frac{AC^2}{AH}=\frac{b^2}{h}AD=AHAC2​=hb2​. Bán kính đường tròn là \dfrac{b^2}{2h}2hb2​.