Question

 Cho tam giác ABC nội tiếp đường tròn (O), đường kính AB = 2R Trên cạnh BC lấy điểm M ( M khác B khác C ) . Đường thẳng AM cắt đường tròn (O) tại điểm D, đường thẳng BD cắt AC tại E. Đường tròn tâm K ngoại tiếp tam giác MBD cắt đường kính AB tại điểm thứ hai N ( N khác B). Đường thẳng CN cắt đường tròn (K) tại F. 
1) Chứng minh DF song song với AE.
2) Chứng minh rằng: BD.BE + AM.AD có giá trị không đổi.    

Answer 1

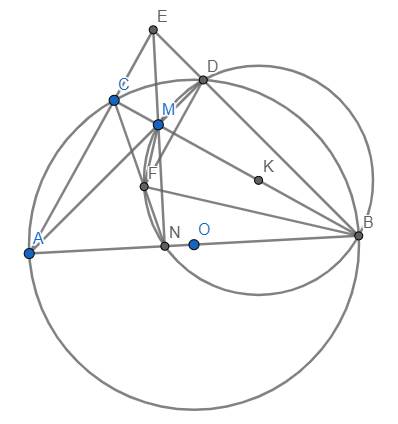
a) Tứ giác BDFN nội tiếp nên \(\widehat{CNA}=\widehat{BDF}\) (*)

 Xét đường tròn (K), đường kính BM, ta có \(\widehat{MNB}=90^o\)  hay \(MN\perp AB\) tại N (1)

 Với lí do tương tự, ta có \(AD\perp EB,BC\perp EA\), do đó M là trực tâm của tam giác EAB \(\Rightarrow EM\perp AB\)  (2)

 Từ (1) và (2) \(\Rightarrow\) M, N, P thẳng hàng và đường thẳng này vuông góc với AB.

 Từ đó suy ra tứ giác BECN nội tiếp (vì \(\widehat{ECB}=\widehat{ENB}=90^o\))

 \(\Rightarrow\widehat{CNA}=\widehat{AEB}\) (**)

Từ (*) và (**), suy ra \(\widehat{BDF}=\widehat{BEA}\) \(\Rightarrow\) DF//AE (đpcm)

b) Tương tự như trên, ta có tứ giác AEDN nội tiếp \(\Rightarrow\widehat{BND}=\widehat{AEB}\), dẫn đến \(\Delta BDN~\Delta BAE\left(g.g\right)\) \(\Rightarrow\dfrac{BD}{BA}=\dfrac{BN}{BE}\Rightarrow BD.BE=BA.BN\) (3)

 Tứ giác NBMD nội tiếp nên \(\widehat{ANM}=\widehat{ADB}\), dẫn đến \(\Delta AMN~\Delta ABD\left(g.g\right)\) 

 \(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AD}\Rightarrow AD.AM=AB.AN\)  (4)

Cộng theo vế (3) và (4), thu được \(BD.BE+AM.AD=AB.BN+AB.AN=AB\left(BN+AN\right)=AB^2=4R^2\)không thay đổi. (đpcm)