Question

Cho tam giác ABC nội tiếp đường tròn (O), A là điểm có định; B, C thay đổi. Kẻ đường cao BH và CK. Chứng minh rằng HK luôn song song với một đường thẳng cố định.

Answer 1

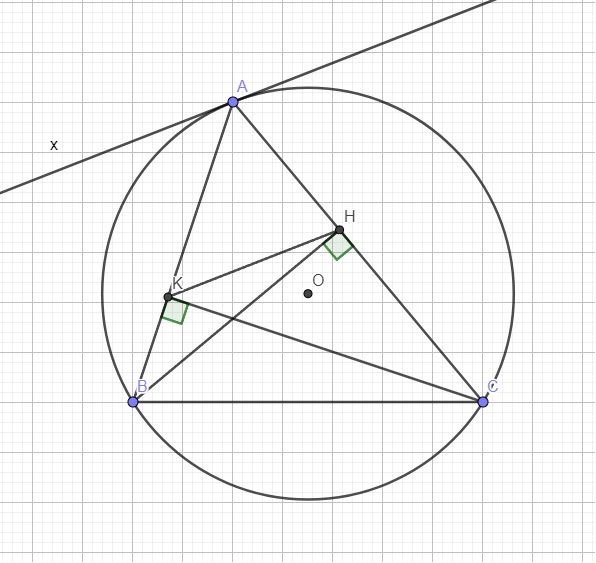
Kẻ tiếp tuyến xy của (O) tại A \(\Rightarrow\) đường thẳng xy cố định (do A và (O) cố định)

H và K cùng nhìn BC dưới 1 góc vuông \(\Rightarrow BCHK\) nội tiếp

\(\Rightarrow\widehat{BKH}+\widehat{ACB}=180^0\)

Mà \(\widehat{BKH}+\widehat{AKH}=180^0\) (kề bù)

\(\Rightarrow\widehat{ACB}=\widehat{AKH}\)

Lại có \(\widehat{ACB}=\widehat{BAx}\) (cùng chắn AB)

\(\Rightarrow\widehat{AKH}=\widehat{BAx}\)

\(\Rightarrow KH||xy\) (hai góc so le trong bằng nhau)

Answer 2