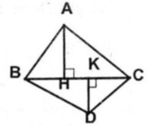
Ta có: \(\left\{{}\begin{matrix}CF\perp AB\left(gt\right)\\AQ||CF\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AQ\perp AB\Rightarrow\widehat{BAC}+\widehat{QAE}=90^0\)
Mà \(\widehat{QAE}+\widehat{AQH}=180^0-\widehat{AEQ}=90^0\)
\(\Rightarrow\widehat{BAC}=\widehat{AQH}\) (1)
Lại có \(\widehat{ACB}=\widehat{QHA}\) (cùng phụ \(\widehat{DAC}\)) (2)
(1);(2) \(\Rightarrow\Delta ABC\sim\Delta QAH\left(g.g\right)\)
\(\Rightarrow\dfrac{QH}{AC}=\dfrac{AH}{BC}\) (3)
Gọi giao điểm của PQ với AD, AM, AC lần lượt là I, J, G
Do \(\left\{{}\begin{matrix}AP||HQ\\AQ||HP\end{matrix}\right.\) (gt) \(\Rightarrow APHQ\) là hình bình hành (tứ giác có 2 cặp cạnh đối song song)
\(\Rightarrow AH\) và PQ cắt nhau tại trung điểm mỗi đường
\(\Rightarrow I\) là trung điểm AH \(\Rightarrow\dfrac{IH}{AH}=\dfrac{1}{2}\)
Do M là trung điểm BC \(\Rightarrow\dfrac{MC}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{IH}{AH}=\dfrac{MC}{BC}\Rightarrow\dfrac{IH}{MC}=\dfrac{AH}{BC}\) (4)
(3);(4) \(\Rightarrow\dfrac{IH}{MC}=\dfrac{QH}{AC}\) (5)
Từ (2) và (5) \(\Rightarrow\Delta IHQ\sim\Delta MCA\left(g.c.g\right)\)
\(\Rightarrow\widehat{IQH}=\widehat{MAC}\)
Mà \(\widehat{IQH}+\widehat{QGE}=180^0-\widehat{QEG}=90^0\)
\(\Rightarrow\widehat{MAC}+\widehat{QGE}=90^0\)
\(\Rightarrow\widehat{MAC}+\widehat{AGJ}=90^0\) (do \(\widehat{QGE}=\widehat{AGI}\) đối đỉnh)
\(\Rightarrow\widehat{AJG}=90^0\)
\(\Rightarrow AM\perp PQ\)