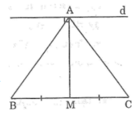
Xét `\triangle ABC` cân tại `A` có: `AM` là đường trung tuyến (`M` là tđ `BC`)
`=>AM` là đường cao của `\triangle ABC`
`=>AM \bot BC`
Mà `d //// BC`
`=> d \bot AM`
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của BC. Vẽ điểm D bất kỳ nằm giữa
M và C, kẻ các đường thẳng qua B và C vuông góc với đường thẳng AD tại H và K . Chứng minh rằng:
a) AM song song BC;
b) Tam giác ABH = Tam giác CAK;
c) Tam giác AHM = Tam giác CKM; d) Tam giác MHK vuông cân.
cho tam giác abc vuông cân tại a 1 đường thẳng song song với bc, cắt tia đối của tia ab,ac lần lượt ở d và e.gọi m là trung điểm của cd
cm:a,tam giác ade vuông cân
b,am vuông góc với be
Cho tam giác ABC cân tại A, góc A < 90 độ.Vẽ BD vuông góc với AC tại D,CE vuông góc với AB tại E. Gọi I là giao điểm của BD và CE.
a)Chứng minh AD=AE
b)Chứng minh AI là tia phân giác cảu góc BAC
c)Chứng minh DE song song với BC
d)Gọi M là trung điểm của BC.Chứng minh A,I,M thẳng hàng
Cho tam giác ABC cân tại A. Gọi H là trung điểm BC
a)Chứng minh tam giác ABH=tam giác ACH và AH là tia phân giác của góc BAC
b)Đường thẳng đi qua điểm H và song song với đường thẳng AC, cắt cạnh AB tại điểm D .Chứng minh tam gíac ADH là tam giác cân.
c) Chứng minh CD< (AC+BC)/2
cho tam giác ABC vuông cân tại A. Một đg thẳng song song với BC, cắt tia đối với các tia AB, AC lần lượt tại E và D. Gọi m là trung điểm của CD .Chứng minh AM vuông góc với BE
Cho tam giác ABC cân tại A, đường trung tuyến AM. Qua A kẻ đường thẳng d vuông góc với AM. Chứng minh rằng d song song với BC.
Cho tam giác ABC có AB < AC, tia phân giác góc A cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AE = AB.
a) Chứng minh: Tam giác BDE là tam giác cân và AD là phân giác của góc BDE.
b) Gọi M là giao điểm của BE và AD. Chứng minh M là trung điểm của BE và AD vuông góc với BE.
c) Qua E vẽ đường thẳng song song với AB và cắt đường thẳng AD tại F. Chứng minh: M là trung điểm của AF.
d) Chứng minh: BF song song với AE.
Cho tam giác ABC vuông cân tại A. Trên cạnh AB,AC lần lượt lấy điểm D và E sao cho AD=AE.Qua A và D kẻ các đường vuông góc với BE cắt BC lần lượt tại M và N. Tia ND cắt tia CA tại I. a) Chứng minh: tam giác AID = tam giác ABE và A là trung điểm IC b) Qua N kẻ đường thẳng song song AC cắt AM tại F. CMR CI=2NF c) Cmr: M là trung điểm mỗi đoạn thẳng AF và NC
