Question

Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Vẽ BP ⊥ MN; CQ ⊥ MN (P, Q Є MN). So sánh S B P Q C   v à   S A B C

A.  S A B C =   2 S C B P Q

B.  S A B C < S C B P Q

C.  S A B C > S C B P Q

D.  S A B C =   S C B P Q

Answer 1

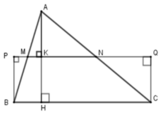
Kẻ AH ⊥ BC tại H và AH cắt MN tại K.

Xét tam giác ABC có MN là đường trung bình nên MN // BC suy ra AH ⊥ MN tại K. Xét tứ giác CBPQ có PQ // BC (do MN // BC) và PB // CQ (do cùng vuông góc với PQ) nên CBPQ là hình bình hành. Lại có P B C ^ = 90⁰ nên tứ giác CBPQ là hình chữ nhật. Suy ra S_CBPQ = BP. BC.

Xét ΔBPM và ΔAKM có:

Suy ra ΔBPM = ΔAKM (ch – gn) => BP = AK (hai cạnh tương ứng) (1)

Xét ΔABK có MK // BH (do MN//BC) và M là trung điểm của AB nên K là trung điểm của AH (định lý về đường trung bình của tam giác). Nên AK = 1 2 AH (2)

Từ (1) và (2) ta có PB =  1 2 AH.

S_ABC =  1 2 AH. BC mà PB = 1 2 AH (cmt) nên S_ABC = PB. BC

Lại có S_CBPQ = BP. BC (cmt) nên ta có S_ABC = S_CBPQ

Đáp án cần chọn là: D