Question

Cho tam giác ABC. Gọi G là trọng tâm tam giác. H là trực tâm tam giác. I là giao điểm 3 đường phân giác. O là điểm cách đều 3 đỉnh tam giác.

Chứng minh rằng: tam giác ABC là tam giác đều khi và chỉ khi các điểm G,H,I,O trùng nhau và ngược lại.

Answer 1

Answer 2

Hình này đc Hông 

Answer 3

Thiên Ngoại Phi Tiên sai rồi cậu lấy trêm mạn mà đúng gì nẫu nói G là trực tâm H là đường cao , o cách đều ba đỉnh mà sao không có ba diểm đó

Answer 4

oh oh sorry, I can't !!!

765784587576

Answer 5

các bạn ơi giúp mình với mình bị Nguyễn Nam Cao ăn cắp nick rồi bạn nào có thể giúp đỡ mình ko

Answer 6

Các Admin ơi hiện nay có một bạn tên là Quản lý Online Math nhưng đây không phải là quản lí mà là Nam Cao Nguyễn bạn ấy thương xuyên bảo chúng mình đặt bảo mật rôi bây giờ cậu ấy lấy nick của Nguyễn Thị Hiện Nhân

Answer 7

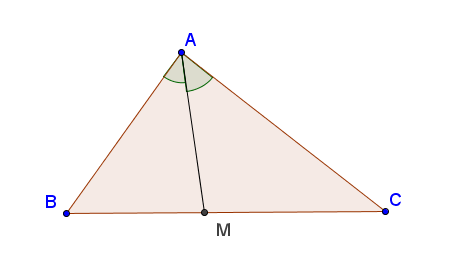
Nobita Kun vẽ hình sai nốt. đề yêu cầu CM tam giác đều mà vẽ tam giác  tù 

Answer 8

hình như cần chứng minh phản chứng nữa thì phải

khi và chỉ khi cho thấy cần xét 5 loại tam giác : cân, tù, nhọn, vuông, đều

Answer 9

Nếu tam giác đó đều thì các đường trung tuyến, đường trung trực, đường phân giác, đường cao trùng nhau. Do đó trọng tâm, trực tâm, giao các đường phân giác, giao các đường trung trực trùng nhau.

Nếu 4 điểm đó = nhau =>tam giacsBAP=BPC( do khi đó các đường phân giác trung trực trung tuyến đường cao trùng nhau)

=>AB=BC

Chứng minh tương tự ta cũng có AB=AC

=> tam giác ABC đều (đpcm).