Bài 9: Tính chất ba đường cao của tam giác
Các câu hỏi tương tự
Bài 1:
a) Cho tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng tam giác đó là tam giác cân.
b) Cho tam giácABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC.
Cho ∆abc vuông tại a có ab=6cm, ac=8cm. Tia phân giác của góc abc cắt ac tại d.
a)Tính bc
b) Kẻ ah vuông góc với bc, tia ah cắt bc tại k. Chứng minh:∆ahb=∆khb
c) Chứng minh:dk vuông góc với bc
d) Qua c kẻ đường thẳng song song với ak, cắt tia ba tại e. Chứng minh:2(ad+ae)>ec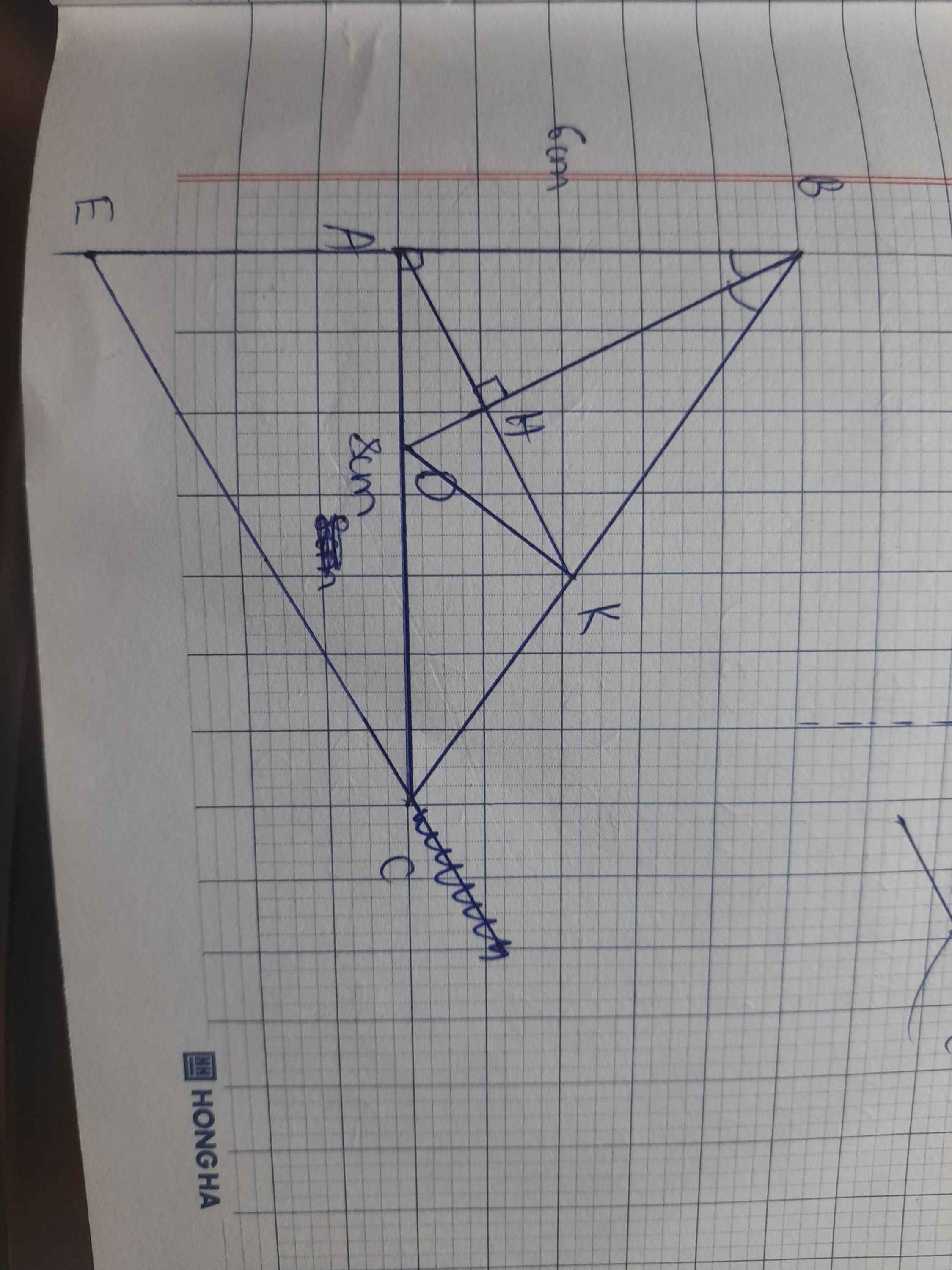
Cho tam giác ABC, AB<AC, trên tia BA và CA lần lượt lấy M và N sao cho BM=CN, trên cạnh AC lấy điểm D sao cho CD=AB. Chứng minh rằng: Ba đường trung trực của AD,MN,BC cùng đi qua một điểm
Cho tam giác ABC vuông tại A . Kẻ tia phân giác BD của góc B ( D thuộc AC ) . Qua D kẻ DE vuông góc BC tại E . a) CM AD = DE . b) Tia ED cắt Tia BA tại F , CM DF = DC . c) CM tam giác AFC cân .
Cho tam giác ABC có AB=AC=5cm BC=6cm đường cao AH xuất phát từ đỉnh A của tam giác ABC (H thuộc BC) a)chứng minh tam giác AHB =AHC b)chứng minh AH là tia phân giác của góc A c)tính độ dài các đoạn thẳng BH và AH
cho tam giác abc vuông tại a có bc=2ab. tia phân giác góc b cắt ac tại .a, chứng minh bd=cd b, tính góc b và góc c của tam giác abc
Cho tam giác ABC vuông tại A. Kẻ đường phân giác BD của tam giác ABC, trên Bc lấy E sao cho BE=BA. a) CM: Tam giác ABD = tam giác EBD và ED vuông góc với BC b) Gọi F là giao điểm của AB và và DE. CM: tam giác BFC cân c) Cho BD cắt FC tại N, trên tia đối NB lấy M sao cho NM=ND. CM: FM // CD. d) Tính chu vi tam giác ABC , biết AB/AC= 3/4 ; BC=15 cm CẦN GẤP :)

Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (h.17)
a) Chứng minh rằng A là trung điểm của EF
b) Các đường cao của tam giác ABC là các đường trung trục của tam giác nào ?
Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC ?










