Question

Cho tam giác ABC, đường trung tuyến AM. Gọi 0 là trung điểm của AM. Qua O kẻ đường thẳng d cắt các cạnh AB, AC. Gọi AA', BB', CC' là các đường vuông góc kể từ A, B, C đến đường thẳng d.

Chứng minh rằng: AA' = (BB' + CC') / 2

Answer 1

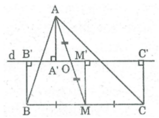
Ta có: BB' ⊥ d (gt)

CC' ⊥ d (gt)

Suy ra: BB'// CC'

Tứ giác BB'C'C là hình thang

Kẻ MM' ⊥ d ⇒ MM' // BB' // CC'

Lại có M là trung điểm của BC nên M' là trung điểm của B’C’

⇒ MM' là đường trung bình của hình thang BB'C'C

⇒ MM' = (BB' + CC') / 2 (1)

* Xét hai tam giác vuông AA'O và MM'O:

∠ (AA'O) =  ∠ (MM' O) = 90 0

AO=MO (gt)

∠ (AOA') =  ∠ (MOM' ) (2 góc đối đỉnh)

Do đó: ∆ AA'O =  ∆ MM'O (cạnh huyền, cạnh góc nhọn)

⇒AA' = MM' (2)

Từ (1) và (2) suy ra: AA' = (BB' + CC') / 2