Các câu hỏi tương tự
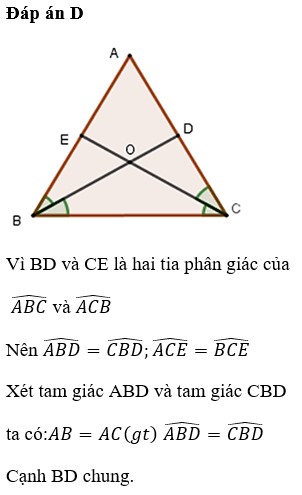
Cho tam giác ABC có ∠B= ∠C. Tia phân giác BD (D ∈ AC) và phân giác CE (E ∈ AB) cắt nhau tại O. Từ O kẻ OH ⊥ AC, OK ⊥ AB. Chứng minh :
a)△ABC=△CBE
b) OB = OC
c) OH = OK
cho tam giác abc cân tại a vẽ phân giác góc b cắt ac tại d phân giác góc c cắt ab tại e . i là giao điểm của bd và ce . cm a , tam giác ibc cân. b, bd=ce
Cho tam giác ABC có góc B = C Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. Gọi K là giao điểm của CE và BD. Chứng minh rằng
a. CE = BD.
Cho tam giác ABC cân tại A. Các đường phân giác BD và CE cắt nhau tại I (D thuộc AC; E thuộc AB). C/minh:
a, BD = CE
b, AI là phân giác của góc A
c, BE = ED = DC
bài 1: cho tam giác ABC vuông tại A có BD là phân giác của góc ABC (D thuộc BC), Tính góc B và góc C biết BDC = 105 độ
Bài 2 : cho tam giác ABC có BD và CE là phân giác của góc B;C (D thuộc AC; E thuộc AB). Góc A=m*. BD cắt CE tại O. Tính góc BOC theo m*
cho tam giác ABC có góc A= 60. Vẽ tia phân giác BD và CE(D thuộc AC; E thuộc AB)cắt nhau tại O
a) Tính góc BOC.
b) Vẽ phân giác ngoài tại B và C cắt nhau tại I. Tính góc BIC.
Cho tam giác ABC cân tại A, qua A vẽ xy //BC, xy cắt các phân giác của góc B và góc C lần lượt tại D và E. Chứng minh:
a) Ax là tia phân giác góc ngoài của tam giác ABC tại A
b) A là trung điểm DE
c) Tam giác CDE vuông
d) BD, CE, FA đồng qui, biết rằng EB và DC cắt nhau tại F
Câu 1: Cho tam giác ABC cắt tia phân giác góc B, C cắt nhau tại I. Qua I kẻ đường thẳng song song với AB cắt AC, BC lần lượt ở D và E. Chứng minh DE=AD+BE
Câu 2:Cho tam giác ABC góc A=60, phân giác BD, CE cắt nhau ở O
Chứng minh: BC=BE+CD
Câu 3: Cho tam giác ABC phân giác trong tại B,C cắt nhau ở O, 2 phân giác góc ngoài tại B,C cắt nhau tại I
Chứng minh: 3 điểm A,O,I thẳng hàng
Cho tam giác ABC cân tại A , BD và CE là tia phân giác của góc B,C (D thuộc AC , E thuộc AB) chúng cắt nhau tại O CMR a, Tam giác ADE cân b, ED // BC c, BE=ED=DC d, OA là trung điểm của góc EOD e, Cho góc A = 40 độ . Tính góc BOC
Bài 1. Cho tam giác ABC cân tại A có Â 80oa) Tính số đo các góc B, C của tam giác ABCb) Tia phân giác của góc B cắt AC tại D. Tính số đo góc ADB.Bài 2. Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC (D ∈ AC), CE vuông góc với AB (E ∈ AB),BD và CE cắt nhau tại I. M là trung điểm BC. Chứng minh:a) ∆BDC CEB.b) Tam giác IBC là tam giác cân.c) IE ID.d) Ba điểm A, I, M thẳng hàng.
Đọc tiếp
 Bài 1. Cho tam giác ABC cân tại A có Â = 80o
Bài 1. Cho tam giác ABC cân tại A có Â = 80o
a) Tính số đo các góc B, C của tam giác ABC
b) Tia phân giác của góc B cắt AC tại D. Tính số đo góc ADB.
Bài 2. Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC (D ∈ AC), CE vuông góc với AB (E ∈ AB),
BD và CE cắt nhau tại I. M là trung điểm BC. Chứng minh:
a) ∆BDC = CEB.
b) Tam giác IBC là tam giác cân.
c) IE = ID.
d) Ba điểm A, I, M thẳng hàng.