Các câu hỏi tương tự
Cho tam giác abcd có o là trung điểm của ac. trên tia bo lấy điểm d sao cho od=ob
a, cm tứ giác abcd là hình bình hành
b, trên cạnh bc lấy các điểm m,n sao cho bm=mn=nc. tia no cắt ad,ab lần lượt tai i và k.cm ai=nc;am song song với in
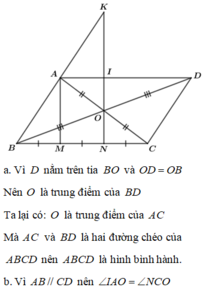
Cho △ABC có O là trung điểm của AC . Trên tia BO lấy điểm D sao cho OD = OB
a) Chứng minh tứ giác ABCD là hình bình hành.
b)Trên cạnh BC lấy các điểm M, N sao cho
BM=MN=NC.Tia NO cắt AD,AB lần lượt tại I
Cho tam giác ABC ,trên cạnh AB và AC lần lượt lấy hai điểm M và N. Biết AM=3cm, BM=2cm, AN=7,5cm , NC=5cm. a) chứng minh rằng MN//BC b) đường trung tuyến AI ( I thuộc BC) của tam giác ABC cắt MN tại K. Chứng minh K là trung điểm của MN
Cho tam giác ABC, các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Trên tia đối của tia NP lấy điểm D sao cho ND NP.a) Chứng minh: Tứ giác ADCP là hình bình hành.b) Gọi F là giao điểm của MN và DC. Giả sử MN 3em. Tinh BC và chứng minh FD FC.c) Gọi H là giao điểm của AP và MN; I là giao điểm của NP và HC. Chứng minh: B, I, F thẳng hàng.nhờ anh chị giải dùm e câu C ạ
Đọc tiếp
Cho tam giác ABC, các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Trên tia đối của tia NP lấy điểm D sao cho ND = NP.
a) Chứng minh: Tứ giác ADCP là hình bình hành.
b) Gọi F là giao điểm của MN và DC. Giả sử MN = 3em. Tinh BC và chứng minh FD = FC.
c) Gọi H là giao điểm của AP và MN; I là giao điểm của NP và HC. Chứng minh: B, I, F thẳng hàng.
nhờ anh chị giải dùm e câu C ạ
Cho tam giác ABC vuông cân tại A, đường trung tuyến AM(M thuộc BC). Lấy điểm P trên cạnh AB sao cho P khác A và B, vẽ đường thẳng song song với BC và AM, hai đường thẳng này cắt AM và BC lần lượt ở N và K.a) Chứng minh PNMK là hình bình hànhb) Trên tia đối của tia MA lấy điểm D sao cho MDMA. Chứng minh ABDC là hình chữ nhậtc) Chứng minh PK+PNAD/2d) Xác định vị trí của điểm P trên cạnh AB để tứ giác PNMK là hình thoie) Tìm điều kiện để tứ giác PNMK là hình vuông
Đọc tiếp
Cho tam giác ABC vuông cân tại A, đường trung tuyến AM(M thuộc BC). Lấy điểm P trên cạnh AB sao cho P khác A và B, vẽ đường thẳng song song với BC và AM, hai đường thẳng này cắt AM và BC lần lượt ở N và K.
a) Chứng minh PNMK là hình bình hành
b) Trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh ABDC là hình chữ nhật
c) Chứng minh PK+PN=AD/2
d) Xác định vị trí của điểm P trên cạnh AB để tứ giác PNMK là hình thoi
e) Tìm điều kiện để tứ giác PNMK là hình vuông
1) Cho tam giác AOB có AB 18cm; OA 12cm; OB 9cm. Trên tia đối của tia OB lấy điểm D sao cho OD 3cm. Qua D kẻ đường thẳng song song với AB cắt tia AO ở C. Gọi F là giao điểm của AD và BC.a) Tính độ dài OC; CDb) Chứng minh rằng FD. BC FC.ADc) Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M và N. Chứng minh: OMON.2) Cho tam giác ABC có AB 8cm; AC 12cm. Trên cạnh AB lấy điểm D sao cho BD 2cm, trên cạnh AC lấy điểm E sao cho AE 9cm.a) Tính các tỉ số AE/AD;AD/ACb) Chứng minh...
Đọc tiếp
1) Cho tam giác AOB có AB = 18cm; OA = 12cm; OB = 9cm. Trên tia đối của tia OB lấy điểm D sao cho OD = 3cm. Qua D kẻ đường thẳng song song với AB cắt tia AO ở C. Gọi F là giao điểm của AD và BC.
a) Tính độ dài OC; CD
b) Chứng minh rằng FD. BC = FC.AD
c) Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M và N. Chứng minh: OM=ON.
2) Cho tam giác ABC có AB = 8cm; AC = 12cm. Trên cạnh AB lấy điểm D sao cho BD = 2cm, trên cạnh AC lấy điểm E sao cho AE = 9cm.
a) Tính các tỉ số AE/AD;AD/AC
b) Chứng minh: tam giác ADE đồng dạng tam giác ABC
c) Đường phân giác của góc BAC cắt BC tại I. Chứng minh: IB.AE = IC.AD
Cho tam giác ABC. trên cạnh AB và AC lần lượt lấy hai điểm M và N biết AM= 3 cm. AM Bằng 7,8 cm .NC = 5 cm a. Chứng minh rằng MN song song với BC b gọi I là điểm trên BC. K là giao điểm của AI và MN cho AC = 6 cm Tính KI
Cho hình vuông ABCD. Trên cạnh AB lấy điểm M, trên tia đối của CB lấy điểm N sao cho AM =CN . Gọi Ilà giao điểm của MN và CD.
GọI E là trung điểm của MN, tia DE cắt BC tại F. Qua M vẽ đường thẳng song song với AD cắt DF tại H. Chứng minh rằng : Tứ giác MFNH là hình thoi.
Chứng minh : Chu vi tam giác BMF không đổi khi m di động trên cạnh AB.
Cho Tam giác ABC cân tại A . Từ một điểm M trên tia AB ( AM < AB ) vẽ đường thẳng song song với BC cắt AC tại N a) Chứng minh tứ giác BMNC là hình thang cân b) Vẽ AE vuông góc với MN . Gọi F , P , Q lần lượt là trung điểm của NC , CB , BM . Chứng minh tứ giác EFPQ là hình thoi . c) MC cắt NB tại I . Chứng minh A , I , P thẳng hàng ( khỏi vẽ hình ạ , giải chi tiết ra hộ tui với ạ)