Ta có MN//BC nên áp dụng đl ta-lét vào tam giác ABC có:
\(\dfrac{AM}{AB}=\dfrac{MN}{BC}=\dfrac{1}{3}=\dfrac{2}{BC}\Rightarrow BC=2:\dfrac{1}{3}=6\left(cm\right)\)
vậy chọn a
Cho tam giác AEC đồng dạng với tam giác ABD như hình vẽ, tính BD:
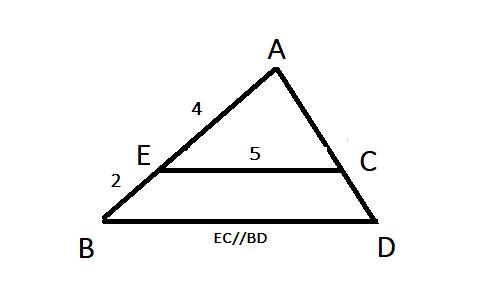
BD bằng:
A. 10 cm
B. 2 cm
C. 4 cm
D. 2,5 cm
Tam giác ABC có AB = 5 cm, AC = 4 cm. Trên cạnh AB lấy điểm M sao cho AM = 3 cm, kẻ MN // BC (N thuộc AC). Tính độ dài đoạn thẳng AN.
Cho cho M N là trung điểm các cạnh AB AC của tam giác ABC khi MN = 8 cm thì
A. AB = 16 cm
B. AC = 16 cm C.
BC = 16 cm
D. BC = AB = AC = 16 cm
Cho tam giác ABC cân tại A, đường phân giác trong của góc C cắt AB tại E và cho biết AC = 20cm, BC = 15cm. Khi đó AE =?
A. 5/4 cm
B. 4/5 cm
C. 80/7 cm
D. 7/80 cm
bài 1 chô tam giác ABCD có M thuộc AB , N thuộc AC biết AB=8 AC=6 BC=10 AM=4 MN=5 chứng minh
a) tam giác AMN đồng dạng tam giác ABC
b) tìm tỉ số đồng dạng
bài 2 cho tam giác ABC đồng dạng tam giác DEF theo tỉ số đồng dạng k1/2 biết AB= 6; AC =8; EF= 20
a, tính chu vi của 2 tam giác
b, cho AD là phân giác góc A tính BD, CD
mik cần gấp mn giúp mik với
bài 1 chô tam giác ABCD có M thuộc AB , N thuộc AC biết AB=8 AC=6 BC=10 AM=4 MN=5 chứng minh
a) tam giác AMN đồng dạng tam giác ABC
b) tìm tỉ số đồng dạng
bài 2 cho tam giác ABC đồng dạng tam giác DEF theo tỉ số đồng dạng k1/2 biết AB= 6; AC =8; EF= 20
a, tính chu vi của 2 tam giác
b, cho AD là phân giác góc A tính BD, CD
Cho hình thoi ABCD có \(\widehat{A}=90^o,^{ }AB=3cm,^{ }AC=4cm.\) Độ dài đường cao kẻ từ A của tam giác bằng:
A. 2,4 cm
B. 3,5 cm
C. 5 cm
D. 7 cm
cho tam giác abc , có ab=10cm , ac=15cm , bc=20 cm ; điểm m thuộc ab, điểm n thuộc ac. sao cho bm=an.và mn // bc. tính bm và mn
Giải giúp mik vs ạ
Thank you ♥️
Cho tam giác ABC có AB = 12cm, AC = 16 cm, BC = 20 cm. 1. Tam giác ABC là tam giác gì? 2. Lấy M, N lần lượt trên AB, AC sao cho AM = 3cm, AN = 4cm. CMR: MN // BC 3. Gọi I là trung điểm BC. G là giao điểm của AI và MN. CMR: G là trung điểm MN
