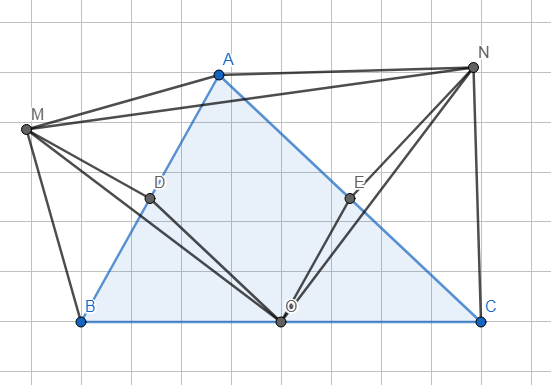
- Sửa đề: \(\Delta ABM,\Delta ACN\) lần lượt vuông cân tại M,N.
- Gọi D, E lần lượt là trung điểm của AB, AC.
- \(\Delta ABM\) vuông cân tại M có: MD là trung tuyến.
\(\Rightarrow MD=\dfrac{AB}{2};\widehat{BDM}=90^0\).
- \(\Delta ACN\) vuông cân tại N có: NE là trung tuyến.
\(\Rightarrow NE=\dfrac{AC}{2};\widehat{CEN}=90^0\).
- \(\Delta ABC\) có: D,E,O lần lượt là trung điểm của AB,AC,BC.
\(\Rightarrow\)OD, OE là đg trung bình của \(\Delta ABC\).
\(\Rightarrow\left\{{}\begin{matrix}OD=\dfrac{AC}{2}\\OE=\dfrac{AB}{2}\end{matrix}\right.\); OD//AC, OE//AB.
\(\Rightarrow OD=NE;OE=MD\)
\(\widehat{ODM}=90^0+\widehat{ODB}=90^0+\widehat{BAC}=90^0+\widehat{OEC}=\widehat{NEO}\).
- \(\Delta ODM\) và \(\Delta NEO\) có:
\(OD=NE\).
\(\widehat{ODM}=\widehat{NEO}\)
\(MD=OE\).
\(\Rightarrow\Delta ODM=\Delta NEO\left(c-g-c\right)\)
\(\Rightarrow MO=NO;\widehat{OMD}=\widehat{NOE}\).
- \(\Delta ODE\) và \(\Delta AED\) có:
\(OD=AE\left(=\dfrac{1}{2}AC\right)\).
\(OE=AD\left(=\dfrac{1}{2}AB\right)\)
\(DE\) là cạnh chung.
\(\Rightarrow\Delta ODE=\Delta AED\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAC}=\widehat{OED}\).
\(\widehat{MON}=\widehat{MOD}+\widehat{ODE}+\widehat{NOE}=\left(\widehat{MOD}+\widehat{OMD}\right)+\widehat{ODE}=180^0-\widehat{ODM}+\widehat{BAC}=180^0-90^0-\widehat{ODB}-\widehat{BAC}=90^0\)
\(\Rightarrow\Delta MON\) vuông tại O mà \(MO=NO\)
\(\Rightarrow\Delta OMN\) vuông cân tại O.













