Em có thể tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath
Em có thể tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath
Cho tam giác abc cố định. Xét các hình chữ nhật có hai đỉnh trên cạnh bc, hai đỉnh còn lại thuộc hai cạnh kia của tam giác. Chứng minh rằng tâm của các hình chữ nhật này thuộc một đoạn cố định.
Không dùng định lý ta-let
Cho tam giác ABC cố định. Xét các hình chữ nhật có 2 đỉnh trên cahj BC, hai đỉnh còn lại thuộc 2 cạnh kia của tam giác. Chứng minh rằng tâm của các hình chữ nhật này thuộc 1 đoạn thẳng cố định
cho tam giác abc cố định xét các hình chữ nhật có hai đỉnh ở trên BC và hai đỉnh kia ở trên hai cạnh còn lại của tam giác. Tìm hình chữ nhật có diện tích lớn nhất
Điền vào chỗ trống:
a) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng bằng 2 cm là ...
b) Tập hợp đỉnh A các tam giác vuông ABC có cạnh huyền BC cố định và BC = 4cm là ...
c) Tập hợp giao điểm O của hai đường chéo của hình chữ nhật ABCD có cạnh BC cố định là ...
Cho tam giác ABC. Trong các hình chữ nhật có 2 đỉnh nằm trên cạnh BC và 2 đỉnh còn lại lần lượt nằm trên 2 cạnh AB,AC.Tìm hình chữ nhật có diện tích lớn nhất
Cho tam giác ABC có cạnh BC cố định Đỉnh A chuyển động trên một đường thẳng song song với BC. CHỨNG MINH RẰNG Trọng tâm G của tam giác chạy trên 1 đường thẳng cố định
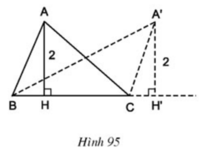
Xét các tam giác ABC có BC cố định, đường cao ứng với cạnh BC luôn bằng 2 cm (h.95). Đỉnh A của các tam giác đó nằm trên đường nào?
cho hình thoi ABCD . P là một điểm trên AB sao cho AP=1/3AB.Q là một điểm trên cạnh CD sao cho CQ=1/3 CD . Gọi I giao điểm của PQ và AD .
a/ tam giác BID là tam giác gì ? vì sao?
b/gọi K là giao điểm của PD và BI . chứng minh K là trung điểm của BI
c/giả sử đỉnh B cố định , đường chéo BD nằm trên đường thẳng Bx cố định , các đỉnh còn lại của hình thoi , di động nhưng luôn có độ dài bằng a không đổi . Chứng minh mỗi điểm D,I,A chuyển động trên một đường cố định
1. Cho hình chữ nhật có chu vi nhở hơn \(2\sqrt{2}\) và 1 tứ giác có các đỉnh nằm trên các cạnh khác nhau của hình chữ nhật đó. Chứng minh chu vi của tứ giác đó không nhỏ hơn 2
2. Cho tam giác ABC có diện tích S độ dài các cạnh a,b,c. Kẻ dường cao AH. Chứng minh rằng: \(S\)≤ \(\dfrac{1}{16}\left(3a^2+2b^2+2c^2\right)\)
3. Cho tam giác ABC vuông cân tại A. M là 1 điểm thay đổi trên BC, hạ MH⊥AB, MK⊥AC (H∈AB, K∈AC). Tìm max \(\left\{MH^4+MK^4\right\}\)