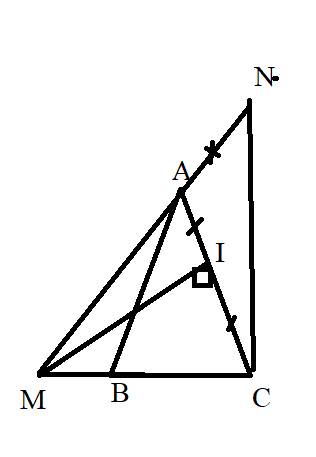
a) Xét 2 tam giác ABN và ANC
AB = AC (1)
BN = NC (2)
AN là cạnh chung (3)
Từ (1) , (2) và (3) => TG ABN = TG ANC ( c-c-c)
Vì ABN = ANC => góc BAN = góc NAC ( cặp góc tương ứng bằng nhau )
Vì BAN = NAC => AM là tia phân giác góc BAC ( đpcm )
b) Bạn tự CM tam giác BaN = tam giác NAC
vì TG BaN = TG NAC => góc BAN = góc NAC
=> AN là p/g góc BAC (a)
mà AM cũng là p/g BAC (b)
Từ (a) ; (b) => A,M,N thẳng hàng (đpcm)
c) Vì TG BAN = TG NAC ( cm câu a )
=> góc BNA = góc ANC
mà BNA và ANC kề bù
=> BNA = ANC = 90 độ
<=> AN vuông góc với BC ( * )
Mà BN = CN ( ** )
Từ ( * ) và ( ** ) => MN là đường trung trực của BC (đpcm)