Đáp án: C
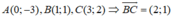
Đường cao kẻ từ A của tam giác ABC là đường thẳng đi qua A và nhận vecto BC là vecto pháp tuyến
⇒ d: 2(x - 0) + (y + 3) = 0 ⇔ 2x + y + 3 = 0
Đáp án: C
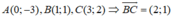
Đường cao kẻ từ A của tam giác ABC là đường thẳng đi qua A và nhận vecto BC là vecto pháp tuyến
⇒ d: 2(x - 0) + (y + 3) = 0 ⇔ 2x + y + 3 = 0
cho tam giác ABC có tọa độ các đỉnh A(1;2), B(3;1) và C(5;4) phương trình nào sau đây là phương trình đường cao của tam giác vẽ từ A.
A. 2x + y + 3 = 0
B. 2x + 3y - 8 = 0
C. 2x + 3y + 8 = 0
D. 3x - 2y + 1 = 0
Cho tam giác ABC và tọa độ một đỉnh và phương trình đường cao.Viết phương trình các cạnh của tam giác đó với:
a, A(3,0),BB'=2x+2y-9=0;CC'=3x-12y-1=0
b,A(1,0), BB'=x-2y+1=0;CC'=3x+y-1=0
Cho tam giác ABC và tọa độ một đỉnh và phương trình đường cao.Viết phương trình các cạnh của tam giác đó với:
a, A(3,0),BB'=2x+2y-9=0;CC'=3x-12y-1=0
b, A(1,0),BB'=x-2y+1=0;CC'=3x+y-1=0
Cho tam giác ABC có đường phân giác trong từ A, trung tuyến từ B, đường cao từ C có phương trình lần lượt là \(x+y-3=0\); \(x-y+1=0\); \(2x+y+1=0\). Tìm tọa độ các đỉnh của tam giác.
Cho Tam giác ABC có A( 4; -2) . Đường cao BH: 2x + y – 4= 0 và đường cao CK: x- y-3= 0. Viết phương trình đường cao kẻ từ đỉnh A.
A.4x+ 5y- 6= 0
B. 4x+ 5y+ 6= 0
C. 4x- 3y+1= 0
D. 3x- 4y+ 7= 0
1. Trong mặt phẳng Oxy cho tam giác ABC có trọng tâm G(−2; 0) biết phương trình các cạnh AB, AC theo thứ tự là 4x+y+14=0; 2x+5y-2=0. Tìm tọa độ các đỉnh A, B, C.
2.Lập phương trình các cạnh AB, AC của tam giác ABC biết đường tuyến CM có phương trình 2x+y-6=0, A(1; 1) và cạnh BC có phương trình x+y-6=0
Cho tam giác ABC , tìm tọa độ các đỉnh của tam giác trong các trường hợp sau a) Biết A(2,2) và hai đường cao có phương trình d1 : x+ y -2 =0 và d2 : 9x-3y+4=0
b) Biết A (4,-1) phương trình đường cao kẻ từ B là d3 : 2x - 3y =0 phương trình trung điểm đi quua điểm d4 : 2x + 3y =0
Cho tam giác ABC có đỉnh A(2;-1), phương trình các đường cao qua B, C lần lượt là 2x-y+1=0 và 3x+y+2=0. Viết phương trình đường trung tuyến AM
Trong mặt phẳng với hệ tọa độ oxy , cho tam giác ABC có đỉnh A(4-1) phương trình đường cao và trung tuyến kẻ từ đỉnh B lần lượt là 2x-3y+12=0 và 3 và 2x-3y=0. Xác định tọa độ các đỉnh còn lại của tam giác ABC