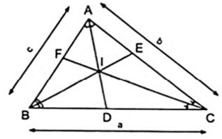
Áp dụng tính chất đường phân giác AD và BI và tam giác ABC và tam giác ABD.
Ta có: DI/IA = DB/AB = BD/c ( 1 )
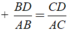
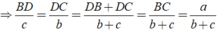
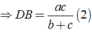
Thay ( 2 ) vào ( 1 ) ta được: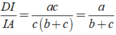
Suy ra: 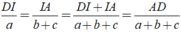
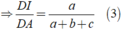

Áp dụng tính chất đường phân giác AD và BI và tam giác ABC và tam giác ABD.
Ta có: DI/IA = DB/AB = BD/c ( 1 )
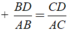
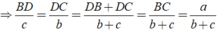
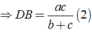
Thay ( 2 ) vào ( 1 ) ta được: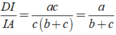
Suy ra: 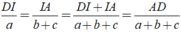
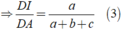
Cho tam giác ABC có BC = a; CA = b; AB = c. Các đường phân giác AD, BE, CF cắt nhau tại I. Chứng minh rằng: D I D A + E I E B + F I F C = 1
Các bạn ơi, cho mình hỏi bài này với:))
Cho tam giác ABC có BC=a; CA=b; AB=c và ba đường phân giác trong AD; BE; CF cắt nhau tại I. Chứng minh:
a) DI/DA=a/(a+b+c)
b) DI/DA+EI/EA+FI/FC=1
Xin cảm ơn!!!
1. Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh:a) H là giao điểm các đường phân giác trong tam giác DEF. b) Gọi M, N, P, Q, I, K lần lượt là trung điểm BC, CA, AB, EF, FD, DE. Chứng minh các đoạn thẳng MQ, NI, PK đồng quy.
2. Cho tam giác ABC cân tại A có AB=AC=b, BC=a. Đường phân giác BD của tam giác ABC có độ dài bằng cạnh bên của tam giác. Chứng minh rằng 1/b−1/a=b/(a+b)^2 ( dấu / là phân số, ^ là mũ).
Bài V:
Cho tam giác nhọn ABC có AB < AC. Ba đường cao AD, BE, CF cắt nhau tại H; AH cắt EF tại I.
a) Chứng minh: D ABE và D ACF đồng dạng; D AEF và D ABC đồng dạng.
b) Vẽ FK ^ BC tại K. Chứng minh: AC.AE = AH.AD và CH.DK = CD.HF.
c) Chứng minh: . EI/ED = HI/HD
d) Gọi M và N lần lượt là trung điểm của đoạn AF và đoạn CD.
Chứng minh: góc BME + góc BNE = 180o
CÁC CA CA,TỈ TỈ ƠI GIÚP MUỘI GIẢI BÀI NÀY VỚI MUỘI ĐANG CẦN GẤP!!!!!!!
Cho tam giác ABC có ba góc nhọn . Các đường cao AD,BE,CF cắt nhau tại H.
a) Chứng minh rằng : BD.DC=DH.DA .
b) Chứng minh rằng: HD/AD+HE/BE+HF/CF=1
c) Chứng minh rằng: H là giao điểm các đường phân giác của tam giác DEF
d) Gọi M,N,P,Q,I,K lần lượt là trung điểm của các đoạn thẳng BC,CA,AB,EF,FD,DE . Chứng minh rằng 3 đường thẳng MQ,NI,PK đồng quy tại một điểm
Cho tam giác nhọn ABC . Các đường cao AD,BE,CF cắt nhau tại H. Chứng minh rằng:
a) Tam giác AEF đồng dạng với tam giác ABC
b) BH.BE + CH.CF = BC2
c) AD.HD < BC2/4
d) Gọi I,K,Q,R lần lượt là chân các đường vuông góc hạ từ E xuống AB,AD ,CF,BC . Chứng minh bốn điểm I,K,Q,R cùng nằm trên một đường thẳng.
Cho tam giác ABC có tia phân giác của góc A cắt BC tại D a) chứng minh AD vuông góc với BC b Vẽ be vuông góc với AC tại E ,BE cắt AD tại I trên tia AB lấy điểm F sao cho AF = AE ,chứng minh IF vuông góc với AB c)Chứng minh c,i,f thẳng hàng
Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H ( D,E,F lần lượt thuộc các cạnh BC, CA, AB). CMR:
a, AF.AB = AH.AD = AE.AC
b, H là giao điểm 3 đường phân giác trong tam giác DEF.
c, Gọi M,N,P,I,K,Q lần lượt là trung điểm của các cạnh BC, AC, AB, EF, ED, DF. CMR:
các đường thẳng MI, NQ, PK đồng quy
d, Gọi độ dài các đoạn thẳng AB, BC, CA lần lượt là a,b,c. Độ dài các đoạn thẳng AD, BE, CF là a', b', c'. Tìm GTNN của biểu thức \(\frac{\left(a+b+c\right)^2}{a'^2+b'^2+c'^2}\)
Bài 10: Cho ABC nhọn có các đường cao AE, CD cắt nhau tại H (E BC, D AB).
a) Chứng minh: ABE ∽ CBD b) Chứng minh: HD . HC = HA.HE c) Nếu BD = 3cm, DC = 4cm. Tính tỉ số AH
DH
Bài 11: Cho tam giác ABC có 3 góc nhọn, các đường cao AD, BE, CF cắt nhau tại H. a) Cm: ABE và ACF đồng dạng. b) Cm: HE.HB = HC.HF c) Cm: góc AEF bằng góc ABC. d) Cm: EB là tia phân giác của góc DEF.