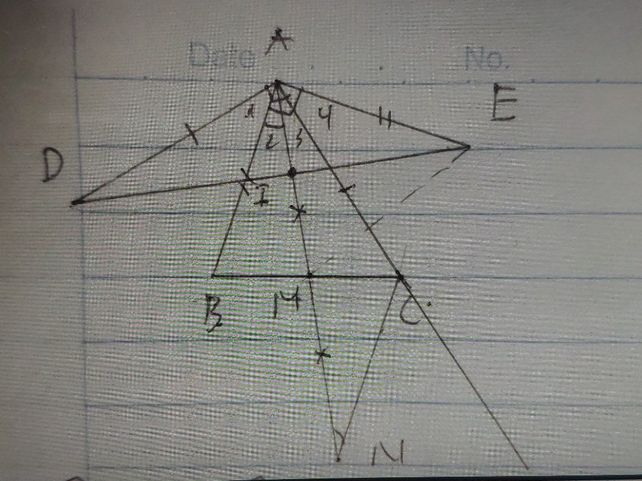
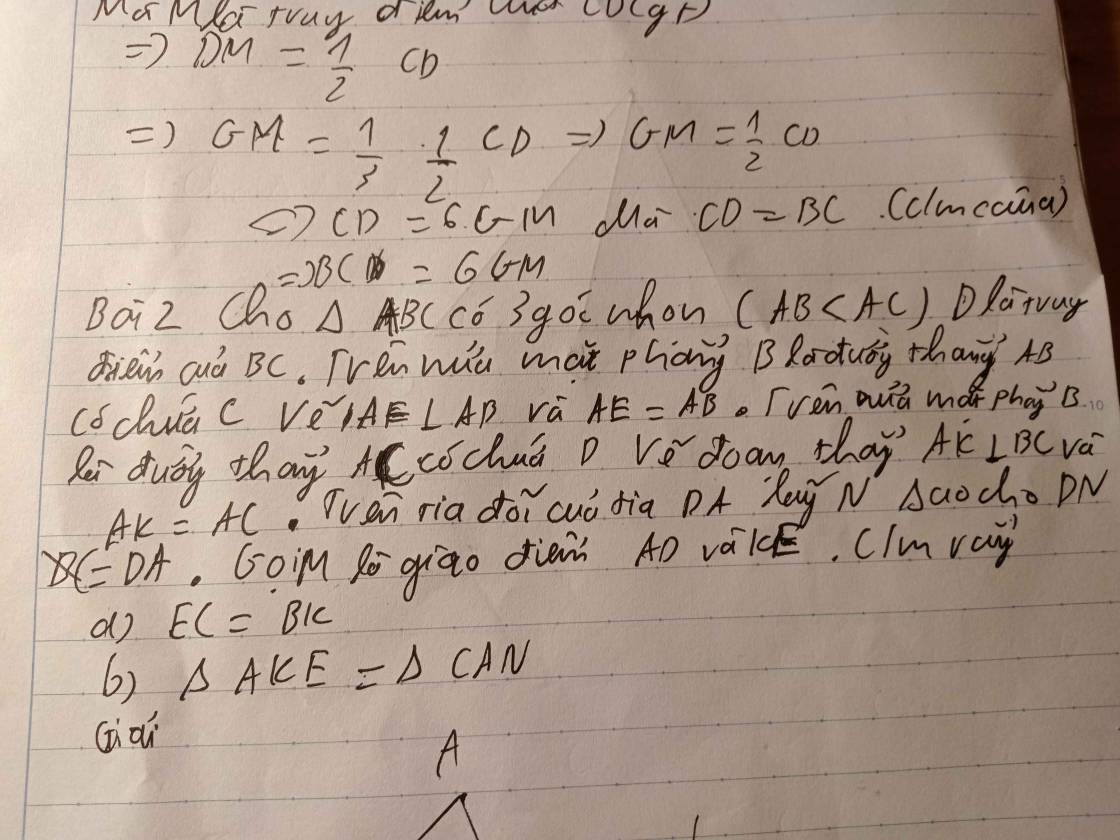Cho tam giác ABC có ba góc nhọn, M là trung điểm của BC. Trên nửa mặt phẳng chứa điểm C bờ là đường thẳng AB vẽ đoạn thẳng AE vuông góc với AB và AE = AB. Trên nửa mặt phẳng chứa điểm B bờ là đường thẳng AC vẽ đoạn thẳng AD vuông góc với AC và AD = AC.
1, Chứng minh rằng BD = CE
2, Trên tia đối của tia MA lấy điểm N sao cho MN = MA. Chứng minh rằng : \(\Delta ADE=\Delta CAN\)
3, Gọi I là giao điểm của DE và AM. Chứng minh rằng \(\frac{AD^2+IE^2}{DI^2+AE^2}=1\)
Bài làm nè bạn nhớ k mình nha