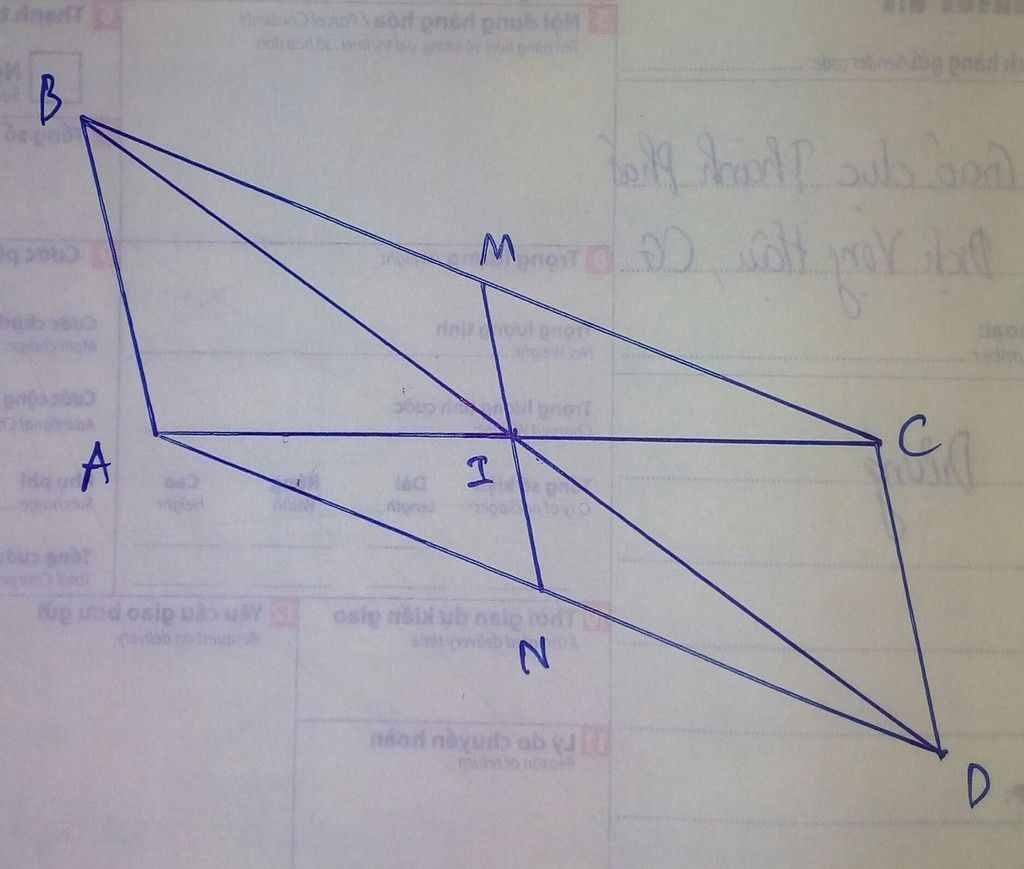
Cho tam giác ABC có A >90 độ. Gọi I là trung điểm của cạnh AC. Trên tia đối của tia IB lấy điểm D sao cho IB=ID. Nối C với D
a, Chứng minh tam giác AIB=tam giác CID
b, Gọi M là trung điểm của BC, N là trung điểm của CD. Chứng minh rằng I là trung điểm của MN
c, Chứng minh AIB góc AIB< góc BIC
d, tìm điều kiện của tam giác ABC để AC vuông góc với CD
thầy giao cho chị làm bài lớp 7 luôn đó
hehehe
em thử làm xem
em đi hok bồi dưỡng toán ko
nếu ko thì khó có thể làm được
heheh Hiếu cố lên em
làm được bài này mới đi thi HSG được đó hem
heheh
a, xét tam giác AIB và tam giác CID có:
IA=IC(gt)
\(\widehat{CID}\)=\(\widehat{AIB}\)( đối đỉnh)
ID=IB(gt)
\(\Rightarrow\)tam giác AIB = tam giác CID(c.g.c)
mik làm câu a, rồi, đến câu b, hình như đề bài bị sai
dạ e sẽ cố cái mẹ m giả nick bố đây con Ayumi phải ko
đúng đó câu b chị cx nghĩ có chỗ sai đó
chị cx ko vẽ được cái I là trung điểm của MN đâu
câu d.
Xét tam giác DIC và BIA
IC = IA
DI = BI
^DIC = ^BIA ( đối đỉnh)
=> tam giác DIC = BIA (c.g.c)
=> ^DCI = ^BAI mà hai góc này ở vị trí so le trong
=> Để AC vuông góc với DC <=> ^DCI = 90
=> ^BAI = 90
Vậy để AC vuông góc với DC thì tam giác ABC là tam giác vuông tại A (Â = 90)
a, xét tam giác ABI và tam giác CDI có
AI = CI ( gt )
góc AIB = góc CID ( đối đỉnh )
BI = ID ( gt)
=> tam giác ABI = tam giác CDI ( c.g.c)
b, theo quan niện của em thì đề là : gọi M là trung điểm của AB , N là trung điểm của CD . chưng minh I là trung điểm của MN
câu b chị nghĩ cái đề này bị lỗi rồi mai lên chị ns vs thầy
chị viết bài khác nữa nha mấy em làm tiếp không
hêheheeheh
giúp chị luôn
có mấy bài chị giải được có mấy câu đầu
b, do tam giác ABI = tam giác CDI
=> AB = CD ( 2 cạnh tương ứng ) và góc ABI = góc CDI ( 2 góc tương ứng )
ta lại có : m là trung điểm cua AB => AM = MB (1)
n là trung điểm của DC => DN = CN (2)
mà AB = CD (3)
từ 1 , 2 và 3 suy ra : AM = BM = DN = CN
xét tam giác MIB và tam giác NID có
BM = DN (cmt)
MBI = NDI ( cmt)
BI = DI (gt)
=> tam giác MIB = tam giác NID (c.gc)
=> góc MIB = góc NID và mi = ni (*)
ta lại có nid + bin = 180 0
mà mib = nid => mib + bin = 180
=> ba điểm n,i,m thẳng hàng (**)
từ (*) và (**) suy ra i là trung điểm của mn
mặt khác
có ai trả lời câu c ko
a.Xét tam giác AIB��� và tam giác CID��� có:
IA=IC��=�� ( gt )
Góc CID��� = Góc AIB��� ( đối đỉnh )
ID=IB��=�� ( gt )
⇒Tam giác AIB��� = Tam giác CID���
→→ AD=BC��=��
b.Ta có Tam giác ABI��� = tam giác CDI���
nên khoảng cách trung tuyến của MI�� và NI�� đều bằng nhau.
⇒ I� là trung điểm của đoạn MN.