Question

cho tam giác ABC có A =90 độ ; đường phân giác BE(E thuộc AC).kẻ EH vuông góc với BC (H thuộc BC ).gọi K là giao  điểm của AB và HE .chứng minh:

a)tam giác ABE=tam giác HBE

b)EK=EC

c)BE vuông góc với AH

d)AE<EC

Answer 1

tham khảo

a) Xét tam giác vuông ABE và tam giác vuông HBE (^BAE = ^BHE = 90^o)

BE chung

^ABE = ^HBE (BE là phân giác ^ABC)

=> tam giác vuông ABE = tam giác vuông HBE (ch - gn)

b) Ta có: AE = HE (tam giác vuông ABE = tam giác vuông HBE)

=> E thuộc đường trung trực của AH (1)

Ta có: AB = HB (tam giác vuông ABE = tam giác vuông HBE)

=> B thuộc đường trung trực của AH (2)

Từ (1) và (2) => BE là đường trung trực của AH (đpcm)

c) Ta có: ^BEK = ^BEA + ^AEK

               ^BEC = ^BEH + ^HEC

Mà ^BEA = ^BEH (tam giác vuông ABE = tam giác vuông HBE)

      ^AEK = ^HEC (2 góc đối đỉnh)

=> ^BEK = ^BEC

Xét tam giác BEK và tam giác BEC: 

^BEK = ^BEC (cmt)

^KBE = ^CBE (BE là phân giác ^ABC)

BE chung

=> tam giác BEK = tam giác BEC (g - c - g)

=> EK = EC (cặp cạnh tương ứng)

 

Answer 2

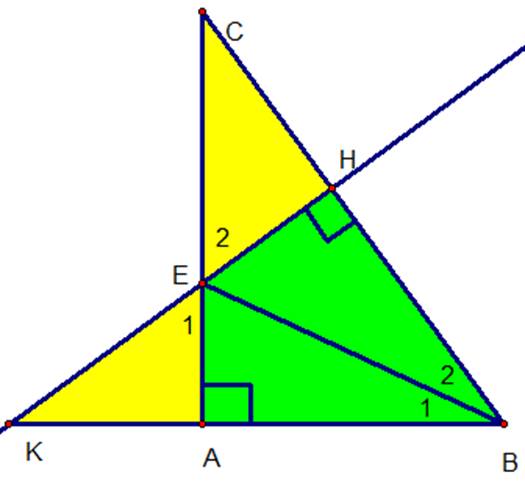
Xét ΔABE và ΔHBE, ta có:

 (gt)

( BE là đường phân giác BE).

BE là cạnh chung.

=> ΔABE = ΔHBE

2. BE là đường trung trực của AH :

BA =BH và EA = EH (ΔABE = ΔHBE)

=> BE là đường trung trực của AH .

3. EK = EC

Xét ΔKAE và ΔCHE, ta có :

 (gt)

EA = EH (cmt)

( đối đỉnh).

=> ΔKAE và ΔCHE

=> EK = EC

4. EC > AC

Xét ΔKAE vuông tại A, ta có :

KE > AE (KE là cạnh huyền)

Mà : EK = EC (cmt)

=> EC > AC.

cre baji