b) Xét tứ giác BFEC có:
∠(BFC) = 90 0 (Do CF là đường cao)
∠(BEC ) = 90 0 (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn
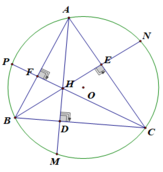
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt nhau tại đường tròn (O) lần lượt tại M, N, P.
Chứng minh rằng:
1: Tứ giác CEHD, nội tiếp.
2: Bốn điểm B, C, E, F cùng nằm trên một đường tròn
3: AE. AC = AH. AD ; AD. BC = BE. AC
4: H và M đối xứng nhau qua BC.
5: Xác định tâm đường tròn nội tiếp tam giác DEF.
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC = AH.AD; AD.BC = BE.AC.H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC = AH.AD; AD.BC = BE.AC.H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC = AH.AD; AD.BC = BE.AC.H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC = AH.AD; AD.BC = BE.AC.H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC = AH.AD; AD.BC = BE.AC.H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.Bài 2:. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC = AH.AD; AD.BC = BE.AC.HELP ME !!!!
Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.
Chứng minh rằng: Tứ giác CEHD, nội tiếp .Bốn điểm B,C,E,F cùng nằm trên một đường tròn.AE.AC = AH.AD; AD.BC = BE.AC.H và M đối xứng nhau qua BC.Xác định tâm đường tròn nội tiếp tam giác DEF.Bài 2. Cho tam giác cân ABC (AB = AC), các đường cao AD, BE, cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác AHE.
Chứng minh tứ giác CEHD nội tiếp .Bốn điểm A, E, D, B cùng nằm trên một đường tròn.Chứng minh ED = 1/2BC.Chứng minh DE là tiếp tuyến của đường tròn (O).Tính độ dài DE biết DH = 2 Cm, AH = 6 Cm.Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M, N, P.
a) Chứng minh tứ giác CEHD nội tiếp
b) Chứng minh 4 điểm B, C, E, F cùng nằm trên một đường tròn
c) Chứng minh AE.AC = AH.AD và AD.BC = BE.AC
d) Chứng minh H và M đối xứng nhau qua BC
e) Xác định tâm đường tròn nội tiếp tam giác DEF
Làm hộ vs !!!!!!!!!!!!!!!!!!!!!!!!!!
