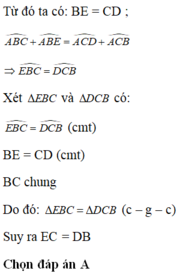Các câu hỏi tương tự
cho tam giác ABC nhọn về phía ngoài của tam giác. Vẽ tam giác đều ACD, nhận AC làm cạnh và tam giác đều ABE, nhận AB làm cạnh.
a) CM: CE=BD
b) Gọi O là giao điểm của BD và CE. Tính số đo góc BOC
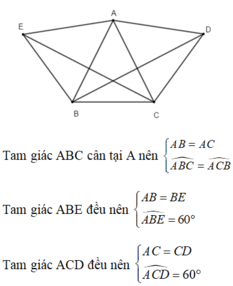
Cho tam giác ABC cân tại A. Vẽ về phía ngoài tam giác ABC các tam giác: ABE, ACD đều.
a, CM tam giác BCD = tam giác CBE.
b, Kẻ AH \(⊥\) BC , H \(\in\) BC . CM AH, CE , BD đồng quy.
Cho tam giác ABC, vẽ về phía ngoài của tam giác ABC các tam giác ABE, ACD vuông tại A và thoả mãn AE = AB; AC = AD. Qua A dựng đường thẳng vuông góc với BC tại H và cắt đoạn thẳng DE tại M. CMR:
a) BD = CE
b) ME = MD
cho tam giác abc cân tại a vẽ phân giác góc b cắt ac tại d phân giác góc c cắt ab tại e . i là giao điểm của bd và ce . cm a , tam giác ibc cân. b, bd=ce
Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng d ở ngoài tam giác ABC. Vẽ BD và CE vuông góc với d. M là trung điểm BC. Chứng minh rằng:
a. BD + CE = DE?
b. Tam giác MDE vuông cân?
CHO TAM GIÁC ABC CÂN TẠI A. VẼ CÁC ĐƯỜNG PHÂN GIÁC BD, CE
a. CMR: BD=CE b. BD CẮT CE TẠI I. CMR: TAM GIÁC BIC CÂN VÀ TAM GIÁC BIE= TAM GIÁC CID
c. CMR:AI VUÔNG GÓC VS ED VÀ ED // BC
Cho tam giác ABC nhọn, vẽ tam giác ngoài ABD vuông cân tại tại A và tam giác ngoài ACE vuông cân tại E.
Chứng minh:
A) BE = CD
B) BE vuông góc với CD
C) BE×BE + CE × CE= DE× DE + BD×BD
Cho ∆ABC vuông tại A (AB < AC). Về phía ngoài ∆ABC vẽ hai tam
giác ABD và tam giác ACE vuông cân ở A.
Chứng minh BC = DE.
Chứng minh BD // CE
cho tam giác ABC cân tại A vẽ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE.a) CM BDCEb) Trên tia CE và BD lần lượt lấy các điểm M và N sao cho E là trung điểm của HM, D là trung điểm của HN. CM: AMAH; tam giác AMN cânc) Tam giác ABC cần cho trước điều kiện gì để tam giác AMN là tam giác đều ?Các bn tìm cách giải câu c giúp mình với. cảm ơn các bn rất nhiều
Đọc tiếp
cho tam giác ABC cân tại A vẽ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE.
a) CM BD=CE
b) Trên tia CE và BD lần lượt lấy các điểm M và N sao cho E là trung điểm của HM, D là trung điểm của HN. CM: AM=AH; tam giác AMN cân
c) Tam giác ABC cần cho trước điều kiện gì để tam giác AMN là tam giác đều ?
Các bn tìm cách giải câu c giúp mình với. cảm ơn các bn rất nhiều