Question

cho tam giác abc cân tại a, đường cao ah. i là trung điểm ah. gọi k là chân đường vuông góc kẻ từ h đến ic. tính akb

Answer 1

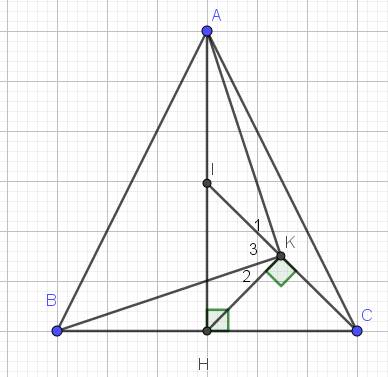
Lời giải:

Vì $ABC$ cân tại $A$ nên đường cao $AH$ đồng thời là đường trung tuyến. Hay $H$ là trung điểm $BC$.

Xét tam giác $IHK$ và $HCK$ có:

$\widehat{IHK}=\widehat{HCK}$ (cùng phụ $\widehat{KHC}$)

$\widehat{IKH}=\widehat{HKC}=90^0$

$\Rightarrow \triangle IHK\sim \triangle HCK$ (g.g)

$\Rightarrow \frac{IH}{HK}=\frac{HC}{CK}$

$\Rightarrow \frac{2IH}{HK}=\frac{2HC}{CK}$

$\Rightarrow \frac{AH}{HK}=\frac{BC}{CK}$

Xét tam giác $BKC$ và $AKH$ có:

$\widehat{BCK}=\widehat{AHK}$ (cùng phụ với góc $\widehat{KHC}$)

$\frac{BC}{KC}=\frac{AH}{HK}$ (cmt)

$\Rightarrow \triangle BKC\sim \triangle AKH$ (c.g.c)

$\Rightarrow \widehat{BKC}=\widehat{AKH}$

$\Rightarrow \widehat{K_2}+90^0=\widehat{K_1}+90^0$
$\Rightarrow \widehat{K_2}=\widehat{K_1}$

$\Rightarrow \widehat{K_2}+\widehat{K_3}=\widehat{K_1}+\widehat{K_3}$

$\Rightarrow \widehat{IKH}=\widehat{AKB}$

Hay $90^0=\widehat{AKB}$

Answer 2

Hình vẽ: