Question

Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh MI = IK = KN.

Answer 1

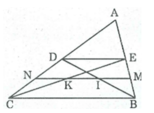
Trong ∆ ABC ta có: E là trung điểm của cạnh AB

D là trung điểm của cạnh AC

Nên ED là đường trung bình của  ∆ ABC

⇒ ED // BC và ED = 1/2 BC

(tính chất đường trung bình của tam giác)

+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.

Trong hình thang BCDE, ta có: BC // DE

M là trung điểm cạnh bên BE

N là trung điểm cạnh bên CD

Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE

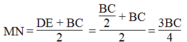
(tính chất đường trung bình hình thang)

Trong  ∆ BED, ta có: M là trung điểm BE

MI // DE

Suy ra: MI là đường trung bình của  ∆ BED

⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)

Trong  ∆ CED ta có: N là trung điểm CD

NK // DE

Suy ra: NK là đường trung bình của  ∆ CED

⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)

IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC

⇒ MI = IK = KN = 1/4 BC