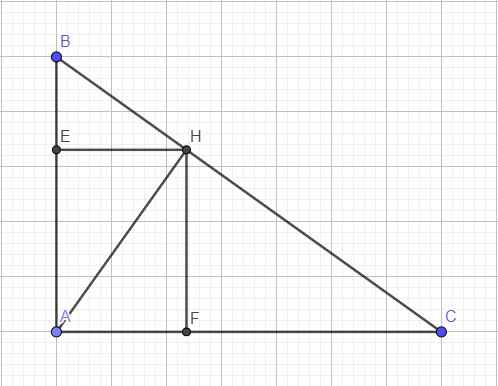
Hệ thức lượng: \(AH^2=BH.CH\)
Hai tam giác vuông BEH và HFC đồng dạng: \(\Rightarrow\dfrac{BE}{FH}=\dfrac{EH}{CF}\Rightarrow BE.CF=EH.FH\)
Hai tam giác vuông AEH và CFH đồng dạng \(\Rightarrow\dfrac{AH}{CH}=\dfrac{EH}{FH}\Rightarrow AH.FH-CH.EH=0\)
Hai tam giác vuông BEH và AFH đồng dạng \(\Rightarrow\dfrac{BH}{AH}=\dfrac{EH}{FH}\Rightarrow EH.AH-BH.FH=0\)
Ta có: \(\left(BE\sqrt{CH}+CF\sqrt{BH}\right)^2=BE^2.CH+CF^2.BH+2BE.CF.\sqrt{BH.CH}\)
\(=BE^2.CH+CF^2.BH+2BE.CF.AH\)
\(=\left(BH^2-EH^2\right)CH+\left(CH^2-FH^2\right)BH+2BE.CF.AH\)
\(=BH.CH\left(BH+CH\right)-EH^2.CH-FH^2.BH+2EH.FH.AH\)
\(=AH^2.BC+EH\left(AH.FH-EH.CH\right)+FH\left(AH.EH-FH.BH\right)\)
\(=AH^2.BC=\left(AH\sqrt{BC}\right)^2\)
\(\Rightarrow BE\sqrt{CH}+CF\sqrt{BH}=AH\sqrt{BC}\)