Vì
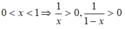
Áp dụng bất đẳng thức Cô – si đối với hai số 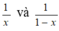 ta được:
ta được:
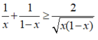
Vì 0 < x < 1 ⇒ 1 - x > 0
Áp dụng bất đẳng thức Cô – si đối với hai số 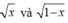 ta được:
ta được:
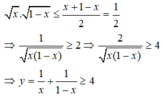
Dấu “ = ” xảy khi và chỉ khi
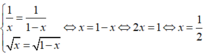
Vậy giá trị nhỏ nhất của hàm số bằng 4 tại x = 1/2
Vì
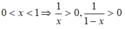
Áp dụng bất đẳng thức Cô – si đối với hai số 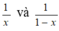 ta được:
ta được:
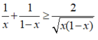
Vì 0 < x < 1 ⇒ 1 - x > 0
Áp dụng bất đẳng thức Cô – si đối với hai số 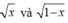 ta được:
ta được:
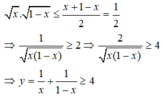
Dấu “ = ” xảy khi và chỉ khi
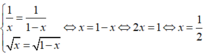
Vậy giá trị nhỏ nhất của hàm số bằng 4 tại x = 1/2
cho số thực dương x;y thỏa mãn x+2y=6 .tìm GTNN của P=\(\dfrac{8}{x}+\dfrac{1}{y}\)
Cho số thực x,y thỏa mãn x+y> bằng 3. Tìm GTNN của biểu thức A=x+y+1/2x +2/y
1. Tìm GTNN Cho x,y là các số thực thỏa mãn x+y=của P=2x3+x3(2y-1)+y3(2x-1)+2y4
Cho 3 số thực dương x,y,z thỏa mãn \(xy+yz+xz\ge3\)> Tìm GTNN của biểu thức
\(P=\frac{x^3}{1+y}+\frac{y^3}{1+z}+\frac{z^3}{1+x}\)
cho hai số thực dương x,y thỏa mãn điều kiện x+y+1=3xy
tìm GTLN của biểu thức P=1/x(y+1) + 1/y(x+1)
Cho x,y,z là 3 số thực dương thỏa mãn đk \(x^2+y^2+z^2=1\). Tìm GTNN của biểu thức
\(P=\frac{x}{y^2+z^2}+\frac{y}{z^2+x^2}+\frac{z}{x^2+y^2}\)
Cho 2 số thực dương x,y thỏa mãn x+y=1. Tìm giá trị nhỏ nhất của biểu thức sau:
Q=x/ căn (1-x) + y/ căn (1-y)
Cho hai số thực dương x,y thõa mãn : x^4+y^4+1/xy=xy + 2
Tìm GTLN VÀ GTNN của P=xy