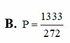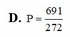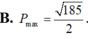Question

Cho số phức z thỏa mãn |z – 1 – 2i| = 2. Giá trị lớn nhất của T = |z| + |z – 3 – 6i| gần với giá trị nào nhất?

A. 6

B. 7

C. 8

D. 9

Answer 1

Chọn C.

Ta có |z|² + |(z – 1 – 2i) + (1 + 2i)|² = |z – 1- 2i|² + |1 + 2i|² + 2(z – 1 – 2i)(1 + 2i)     (1)

|z – 3 – 6i|² = |(z – 1 – 2i) – 2(1 + 2i)|² = |z – 1 – 2i|² + 4|1 + 2i|² - 4(z – 1- 2i)(1 + 2i)   (2)

Từ (1) và (2) suy ra: 2|z|² + |z – 3- 6i|² = 3|z – 1- 2i|² + 6|1 + 2i| = 12 + 30 = 42.

Áp dụng bất đẳng thức Bunhiakovsky ta có:

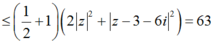
Vậy