Các câu hỏi tương tự
Cho số phức z thỏa mãn điều kiện
2
+
i
z
+
1
-
i
1
+
i
5
-
i
.
Môđun của số phức
w
1
+
2
z
+
z
2
có giá trị là A. 10. B. 25 C. 100. D. 40
Đọc tiếp
Cho số phức z thỏa mãn điều kiện 2 + i z + 1 - i 1 + i = 5 - i . Môđun của số phức w = 1 + 2 z + z 2 có giá trị là
A. 10.
B. 25
C. 100.
D. 40
Cho số phức z thỏa mãn điều kiện
2
+
i
z
+
1
-
i
1
+
i
5
-
i
Môđun của số phức
w
1
+
2
z
+
z
2
có giá trị là A. -10 B. 100 C. -100 D. 1...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện 2 + i z + 1 - i 1 + i = 5 - i Môđun của số phức w = 1 + 2 z + z 2 có giá trị là
A. -10
B. 100
C. -100
D. 10
Trong các số phức z thỏa mãn
z
2
+
1
2
z
, gọi
z
1
và
z
2
lần lượt là các số phức có môđun lớn nhất và nhỏ...
Đọc tiếp
Trong các số phức z thỏa mãn z 2 + 1 = 2 z , gọi z 1 và z 2 lần lượt là các số phức có môđun lớn nhất và nhỏ nhất.
Khi đó môđun lớn nhất của số phức w = z 1 + z 2 là:
A. w = 2 2
B. w = 2
C. w = 2
D. w = 1 + 2
Cho số phức z có phần thực là số nguyên và z thỏa mãn
z
-
2
z
-
7
+
3
i
+
z
. Môđun của số phức
w
1
-
z
+
z
2
bằng A.
w
445
B.
w...
Đọc tiếp
Cho số phức z có phần thực là số nguyên và z thỏa mãn z - 2 z = - 7 + 3 i + z . Môđun của số phức w = 1 - z + z 2 bằng
A. w = 445
B. w = 425
C. w = 37
D. w = 457
Cho số phức z thỏa mãn điều kiện
z
-
3
+
2
i
z
-
i
Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
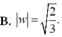
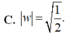
![]()
Trong các số phức z thỏa mãn
z
2
+
1
2
z
, gọi
z
1
và
z
2
lần lượt là các số phức có môđun lớn nhất và nhỏ nhất. Khi đó môđun lớn nhất của số phức
w
...
Đọc tiếp
Trong các số phức z thỏa mãn z 2 + 1 = 2 z , gọi z 1 và z 2 lần lượt là các số phức có môđun lớn nhất và nhỏ nhất. Khi đó môđun lớn nhất của số phức w = z 1 + z 2 là:
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn điều kiện:
z
-
1
+
2
i
5
và
w
z
+
1
+
i
có môđun lớn nhất. Số phức z có môđun bằng: A.
2
5
B.
3
2
C.
6
D.
5
2
Đọc tiếp
Cho số phức z thỏa mãn điều kiện: z - 1 + 2 i = 5 và w = z + 1 + i có môđun lớn nhất. Số phức z có môđun bằng:
A. 2 5
B. 3 2
C. 6
D. 5 2
Cho số phức z thỏa mãn điều kiện:
z
-
1
+
2
i
5
và w z +1 +i có môđun lớn nhất. Số phức z có môđun bằng: A.
6
B.
3
2
C.
5
2
D.
2
5
Đọc tiếp
Cho số phức z thỏa mãn điều kiện: z - 1 + 2 i = 5 và w = z +1 +i có môđun lớn nhất. Số phức z có môđun bằng:
A. 6
B. 3 2
C. 5 2
D. 2 5
Cho số phức z thỏa mãn
z
+
3
i
+
z
-
3
i
10
. Gọi
M
1
;
M
2
lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của
M
1...
Đọc tiếp
Cho số phức z thỏa mãn z + 3 i + z - 3 i = 10 . Gọi M 1 ; M 2 lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của M 1 M 2 , M(a, b) biểu diễn số phức w, tổng a + b nhận giá trị nào sau đây?
A. 7 2
B. 5
C. 4
D. 9 2




