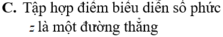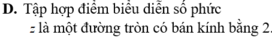Chọn B.
Ta có : 11z10 + 10iz9 + 10iz - 11 = 0.
Hay z9( 11z + 10i) = 11 - 10iz
Hay: 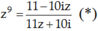
Đặt z = x + yi. Từ (*) suy ra:
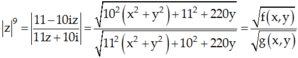
Xét các trường hợp:
+ Nếu |z| > 1 thì x2 + y2> 1 nên:G( x; y) =11( x2 + y2) + 102 +220y = 102( x2 + y2) + 21( x2 + y2) + 102 + 220y > 102( x2 + y2) + 112 + 220y = f( x; y)
Do đó |z9 | < 1 ⇒ z < 1 (mâu thuẫn).
+ Nếu |z| < 1 thì x2 + y2 > 1 nên:
G( x; y) = 11( x2 + y2) + 102+220y = 102( x2+ y2) + 21( x2 + y2) + 102+ 220y < 102( x2 + y2) + 112+ 220y = f( x; y)
Suy ra |z9| > 1 ⇒ |z| > 1 (mâu thuẫn).
+ Nếu |z| = 1 thì g( x; y) = f( x; y) (thỏa mãn)
Vậy |z| = 1.






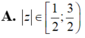
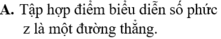



 . Tìm khẳng định đúng
. Tìm khẳng định đúng