Đáp án A
Đặt ![]() vì z có phần ảo âm suy ra y < 0. Khi đó
vì z có phần ảo âm suy ra y < 0. Khi đó
![]()
![]()
![]()
Vậy w là một số thực.
Đáp án A
Đặt ![]() vì z có phần ảo âm suy ra y < 0. Khi đó
vì z có phần ảo âm suy ra y < 0. Khi đó
![]()
![]()
![]()
Vậy w là một số thực.
Biết z là số phức có phần ảo âm và là nghiệm của phương trình z 2 - 6 z + 10 = 0 Tính tổng phần thực và phần ảo của số phức w = z z ¯
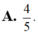
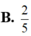
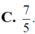
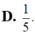
Kí hiệu z 0 là nghiệm phức có phần thực âm và phần ảo dương của phương trình z 2 + 2 z + 10 = 0 Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = t 2017 z 0
![]()
![]()
![]()
![]()
Kí hiệu Z 0 là nghiệm phức có phần thực âm và phần ảo dương của phương trình z 2 + 2z + 10 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = i 2017 z 0 ?
A. M(3;-1)
B. M(3;1)
C. M(-3;1)
D. M(-3;-1)
Kí hiệu z 0 là nghiệm phức có phần thực âm và phần ảo dương của phương trình z 2 + 2z + 10 = 0. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = i 2017 z 0 ?
A. M(3;-1)
B. M(3;1)
C. M(-3;1)
D. M(-3;-1)
Cho số phức z = 4 + 2i Phần thực và phần ảo của w = 2 z - i là
A. Phần thực là 8, phần ảo là 3i
B. Phần thực là 8, phần ảo là 3
C. Phần thực là 8, phần ảo là -3i
D. Phần thực là 8, phần ảo là 3
Cho số phức z có phần thực và phần ảo đều khác 0. Khi đó số phức z và w= - z ¯ được biểu diễn hình học bởi 2 điểm M, N thì M và N:
A. Đối xứng qua gốc O
B. Đối xứng qua Oy
C. Đối xứng qua Ox
D. Cả A, B, C đều sai
Cho số phức z = 10i - 8 Tìm phần thực, phần ảo của số phức w = z - i
A. Phần thực bằng -8 và phần ảo bằng -8i
B. Phần thực bằng -2 và phần ảo bằng -3
C. Phần thực bằng 8 và phần ảo bằng 10i
D. Phần thực bằng – 8 và phần ảo bằng 9
Cho z là số phức thỏa mãn điều kiện 2 z − 1 1 + i + z ¯ + 1 1 − i = 2 − 2 i . Tính tổng bình phương phần thực và phần ảo của số phức w = 9 z 2 + 6 z + 1
A. 25
B. 1
C. 49
D. 41
Gọi z 0 là nghiệm phức có phần ảo âm của phương trình z 2 + 2 z + 5 = 0 . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức w = i 2019 z 0 ?
![]()
![]()
![]()
![]()