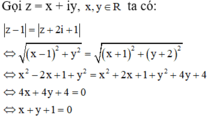Các câu hỏi tương tự
Cho số phức z
1
+
i
5
. Điểm biểu diễn số phức z nằm trong góc phần tư nào của hệ tọa độ vuông góc của mặt phẳng phức? A. Góc phân tư thứ IV B. Góc phân tư thứ I C. Góc phân tư thứ II D. Góc phân tư thứ III
Đọc tiếp
Cho số phức z = 1 + i 5 . Điểm biểu diễn số phức z nằm trong góc phần tư nào của hệ tọa độ vuông góc của mặt phẳng phức?
A. Góc phân tư thứ IV
B. Góc phân tư thứ I
C. Góc phân tư thứ II
D. Góc phân tư thứ III
Cho hai số phức α = a + bi, β = c + di. Hãy tìm điều kiện của a, b, c, d để các điểm biểu diễn α và β trên mặt phẳng tọa độ: Đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất và góc phần tư thứ ba
Cho hai số phức α a + bi, β c + di. Hãy tìm điều kiện của a, b, c, d để các điểm biểu diễn α và β trên mặt phẳng tọa độ:a) Đối xứng với nhau qua trục Ox ;b) Đối xứng với nhau qua trục Oy;c) Đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất và góc phần tư thứ ba;d) Đối xứng với nhau qua gốc tọa độ.
Đọc tiếp
Cho hai số phức α = a + bi, β = c + di. Hãy tìm điều kiện của a, b, c, d để các điểm biểu diễn α và β trên mặt phẳng tọa độ:
a) Đối xứng với nhau qua trục Ox ;
b) Đối xứng với nhau qua trục Oy;
c) Đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất và góc phần tư thứ ba;
d) Đối xứng với nhau qua gốc tọa độ.
Cho số phức z thỏa mãn
z
.
z
13
Biết M là điểm biểu diễn số phức z và M thuộc đường thẳng y -3 nằm trong góc phần tư thứ ba trên mặt phẳng Oxyz. Khi đó môđun của số phức
w
z
-
3
+
15
i
bằng bao nhiêu?
Đọc tiếp
Cho số phức z thỏa mãn z . z = 13 Biết M là điểm biểu diễn số phức z và M thuộc đường thẳng y = -3 nằm trong góc phần tư thứ ba trên mặt phẳng Oxyz. Khi đó môđun của số phức w = z - 3 + 15 i bằng bao nhiêu?
![]()
![]()
![]()
![]()
Gọi M là điểm biểu diễn số phức
w
2
z
+
z
¯
+
1
-
i
z
2
+
i
, trong đó z là số phức thỏa mãn
(
1
-
i
)
(
z
-...
Đọc tiếp
Gọi M là điểm biểu diễn số phức w = 2 z + z ¯ + 1 - i z 2 + i , trong đó z là số phức thỏa mãn ( 1 - i ) ( z - i ) = 2 - i + z . Gọi N là điểmtrong mặt phẳng sao cho ( O x → , O N → ) = 2 ρ , trong đó ρ = ( O x → , O M → ) là góc lượng giác tạo thành khi quay tia Ox tới vị trí tia OM. Điểm N nằm trong góc phần tư nào?
![]()
![]()
![]()
![]()
Cho hàm số có đồ thị
(
C
m
)
và A là điểm cố định có hoành độ âm của
(
C
m
)
. Giá trị của để tiếp tuyến tại A của
(
C
m
)
vuông góc với đường phân giác góc phần tư thứ nhất là A. B. C. D.
Đọc tiếp
Cho hàm số 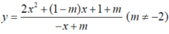 có đồ thị
(
C
m
)
và A là điểm cố định có hoành độ âm của
(
C
m
)
. Giá trị của để tiếp tuyến tại A của
(
C
m
)
vuông góc với đường phân giác góc phần tư thứ nhất là
có đồ thị
(
C
m
)
và A là điểm cố định có hoành độ âm của
(
C
m
)
. Giá trị của để tiếp tuyến tại A của
(
C
m
)
vuông góc với đường phân giác góc phần tư thứ nhất là
A.![]()
B. ![]()
C. ![]()
D. 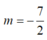
Biết rằng ba điểm A, B, C lần lượt là các điểm biểu diễn hình học của số phức z1=1-2i, z2=3+i, z3=-2-2i. Tìm tọa độ đỉnh thứ tư của hình bình hành ABCD.
A. D(-6;-5)
B.D(-6;-3)
C.(-4;-3)
D.D(-4;-5)
Cho số phức z1, z2 thỏa mãn
z
1
z
2
2
5
. Gọi M, N lần lượt là điểm biểu diễn hai số phức z1, z2 trên mặt phẳng tọa độ. Biết
M
N
2
2
. Gọi H là đỉnh thứ tư của hình bình hành OMHN và K là trung điểm của OM. Tính lKH.
Đọc tiếp
Cho số phức z1, z2 thỏa mãn z 1 = z 2 = 2 5 . Gọi M, N lần lượt là điểm biểu diễn hai số phức z1, z2 trên mặt phẳng tọa độ. Biết M N = 2 2 . Gọi H là đỉnh thứ tư của hình bình hành OMHN và K là trung điểm của OM. Tính l=KH.
![]()
![]()
![]()
![]()
Trên mặt phẳng tọa độ, các điểm A, B, C theo thứ tự biểu diễn các số phức 2+3i, 3+i, 1+2i.Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z
A. z=1+i
B.z=2+2i
C.z=2-2i
D.z=1-i