Các câu hỏi tương tự
Cho z, w là 2 số phức được biểu diễn bởi hai điểm đối xứng nhau qua trục Oy. Biết z = 1 + 2i. Tìm w
A. w = 1-2i
B. w = -1+2i
C. w = 2 + i
D. w = 2 - i
Hai số phức z = -1+2i và w = -2+i được biểu diễn bởi hai điểm M, N thì M và N là hai điếm đối xứng nhau qua đường thẳng
A. x = 0
B. y = 0
C. y = x
D. y = -x
z = -1 + i được biểu diễn bởi điểm M trong mặt phẳng Oxy. Biết điểm M' biểu diễn số phức w và M’ đối xứng với M qua đường thẳng: ∆ : x-y+1 = 0. Tìm w.
A. w = 0
B. w = 1-i
C. w = 1+i
D. w = -2+2i
Cho các số phức z-1+2i,w2-i. Điểm nào trong hình bên biểu diễn số phức z+w? A.N B.P C.Q D.M
Đọc tiếp
Cho các số phức z=-1+2i,w=2-i. Điểm nào trong hình bên biểu diễn số phức z+w?
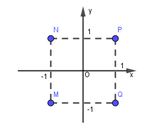
A.N
B.P
C.Q
D.M
Cho z = 1 - 2i. Tìm số phức sao cho khi biểu diễn z và w trên mặt phẳng tọa độ ta được hai điểm đối xứng nhau qua trục Oy.
A. w = 1 + 2i
B. w = -1 + 2i
C. w = -1 - 2i
D. w = -2 + i
Cho hai số phức w và z thỏa mãn
w
-
1
+
2
i
z
. Biết tập hợp các điểm biểu diễn của số phức z là đường tròn tâm I(-2;3) bán kính r 3. Tìm tập hợp các điểm biểu diễn của số phức A. Là một đường thẳng song song trục tung B. Là một đường thẳng không song song với trục tung C. Là đường tròn, tọa độ tâm (-3;5) bán kính bằng
3
5...
Đọc tiếp
Cho hai số phức w và z thỏa mãn w - 1 + 2 i = z . Biết tập hợp các điểm biểu diễn của số phức z là đường tròn tâm I(-2;3) bán kính r = 3. Tìm tập hợp các điểm biểu diễn của số phức
A. Là một đường thẳng song song trục tung
B. Là một đường thẳng không song song với trục tung
C. Là đường tròn, tọa độ tâm (-3;5) bán kính bằng 3 5
D. Là đường tròn, tọa độ tâm (-1;1) bán kính bằng 3
Cho số phức z = 3 - 2i. Tìm điểm biểu diễn của số phức w = z + i. z ¯
A. M(1;1)
B. M(1;-5)
C. M(5;-5)
D. M(5;1)
Cho số phức z = 3 - 2i Tìm điểm biểu diễn của số phức w = z + i. z ¯
A. M(1;1)
B. M(1;-5)
C. M(5;-5)
D. M(5;1)
Cho w là số phức thay đổi thỏa mãn
w
2
. Trong mặt phẳng phức, các điểm biểu diễn số phức z3w+1-2i chạy trên đường nào? A. Đường tròn tâm I(1;-2), bán kính R6 B. Đường tròn tâm I(-1;2), bán kính R2 C. Đường tròn tâm I(1;-2), bán kính R2 D. Đường tròn tâm I(-1;2), bán kính R6
Đọc tiếp
Cho w là số phức thay đổi thỏa mãn w = 2 .
Trong mặt phẳng phức, các điểm biểu diễn số phức z=3w+1-2i chạy trên đường nào?
A. Đường tròn tâm I(1;-2), bán kính R=6
B. Đường tròn tâm I(-1;2), bán kính R=2
C. Đường tròn tâm I(1;-2), bán kính R=2
D. Đường tròn tâm I(-1;2), bán kính R=6



