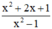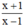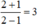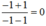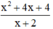a) Với giá trị của x thì phân thức được xác định là : \(x^2-1\ne0\)
=> \(x^2\ne\pm1\)
b) Rút gọn A : \(A=\frac{x^2+2x+1}{x^2-1}=\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}=\frac{x+1}{x-1}\)
c) Tại x = -2 thì \(A=\frac{\left(-2\right)+1}{\left(-2\right)-1}=\frac{-1}{-3}=\frac{1}{3}\)
d) Ta có : \(A=\frac{x^2+2x+1}{x^2-1}=\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=1+\frac{2}{x-1}\)
=> \(2⋮x-1\)=> x - 1 \(\in\)Ư(2) = { \(\pm1;\pm2\)}
+) x - 1 = 1 => x = 2 ; x - 1 = -1 => x = 0
+) x - 1 = 2 => x = 3 ; x - 1 = -2 => x = -1
Vậy : ....
a) Phân thức xác định
\(\Leftrightarrow x^2-1\ne0\)
\(\Leftrightarrow x\ne\pm1\)
Vậy với \(x\ne\pm1\)thì giá trị của phân thức đã cho xác định.
b) \(A=\frac{x^2+2x+1}{x^2-1}\)
\(\Leftrightarrow A=\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow A=\frac{x+1}{x-1}\)
c) x = -2 ( thỏa mãn đkxđ )
Vậy \(A=\frac{-2+1}{-2-1}=\frac{-1}{-3}=\frac{1}{3}\)
d) A có giá trị nguyên
\(\Leftrightarrow\frac{x+1}{x-1}\)có giá trị nguyên
\(\Leftrightarrow\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=1+\frac{2}{x-1}\)có giá trị nguyên
\(\Leftrightarrow x-1\inƯ\left(2\right)\)
\(\Leftrightarrow x=\left\{2;3;0\right\}\)
\(A=\frac{x^2+2x+1}{x^2-1}\)
a) ĐKXĐ : \(x^2-1\ne0\Rightarrow x\ne\pm1\)
b) \(A=\frac{x^2+2x+1}{x^2-1}=\frac{\left(x+1\right)^2}{\left(x+1\right)\left(x-1\right)}=\frac{x+1}{x-1}\)
c) Thế x = -2 ( tmđk ) vào A ta được :
\(A=\frac{-2+1}{-2-1}=\frac{-1}{-3}=\frac{1}{3}\)
Vậy A = 1/3 khi x = -2
d) \(A=\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=1+\frac{2}{x-1}\)
Để A nguyên => \(\frac{2}{x-1}\)nguyên
=> \(2⋮x-1\)
=> \(x-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
=> \(x\in\left\{2;0;3;-1\right\}\)