Các câu hỏi tương tự
Cho đường tròn (O;R), đường kính AB .Gọi C là điểm chính giữa của cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm BOD. Có mấy đáp số
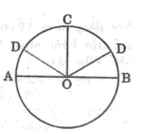
Cho đường tròn (O; R), đường kính AB. Gọi C là điểm chính giữa của cung AB. Vẽ dây CD dài bằng R. Tính góc ở tâm DOB. Có mấy đáp số ?
Cho (O;R) AB là đường kính, C là điểm nằm chính giữa của cung AB, vẽ dây CD=R. Tính sđ cung BD
Cho đường tròn tâm o bán kính R, đường kính MN. Gọi P là điểm chính giữa của cũng MN, vẽ dây PQ = R. Tính số đo góc tâm NOQ Q € cung nhỏ NP
Cho đường tròn tâm O đường kính AB2R. Vẽ dây cung CD vuông góc với AB tại I(I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC(E khác B và C), AE cắt CD tại Fa) Chứng minh tứ giác BEFL nội tiếp trong một đường trònb) Tính độ dài cạnh AC theo R và góc ACD khi góc BAC60độc) Chứng minh khi điểm E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp tam giác CEF luôn thuộc một đường thẳng cố định
Đọc tiếp
Cho đường tròn tâm O đường kính AB=2R. Vẽ dây cung CD vuông góc với AB tại I(I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC(E khác B và C), AE cắt CD tại F
a) Chứng minh tứ giác BEFL nội tiếp trong một đường tròn
b) Tính độ dài cạnh AC theo R và góc ACD khi góc BAC=60độ
c) Chứng minh khi điểm E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp tam giác CEF luôn thuộc một đường thẳng cố định
Cho đường tròn tâm O bán kính R và dây AB. Vẽ đường kính CD vuông góc với AB tại K. M là điểm thuộc cung nhỏ BC. Gọi F là giao điểm của DM và AB.
a) Chứng minh rằng tứ giác CKFM là tứ giác nội tiếp
b) Chứng minh rằng: \(AD^2\) = DF. DM
Cho đường tròn (O) đường kính AB. Vẽ dây CD không qua tâm vuông góc với AB tại I (A thuộc cung nhỏ CD) biết CD=16cm ; IA=6cm. Tính bán kính của (O;R)
Cho đường tròn (O;R) với dây BC cố định ( BC không đi qua O). Gọi A là điểm chính giữa cung nhỏ BC. Điểm E thuộc cung lớn BC. Nối AE cắt dây BC tại D. Gọi I là trung điểm dây BC. Hạ CH vuông góc với AE. đường thẳng BE cắt CH tại M
b) Chứng minh AD.AE= AB2
c) Cho BC = R căn 3. Tính AC
Cho (O;R) có hai dây cung AB, AC tùy ý ( O nằm trong góc BAC) kẻ đường kính AD
a) cm: góc BAD= góc BCD và BD vuông góc AB
b) Lấy E thuộc (O) sao cho điểm D là điểm chính giữa của cung nhỏ BE. Cm: CD là phân giác của góc BCF











