Các câu hỏi tương tự
Cho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng 1200? A.
M
N
→
,
N
P
→
B.
M
O...
Đọc tiếp
Cho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng 1200?
A. M N → , N P →
B. M O → , O N → .
C. M N → , O P → .
D. M N → , M P → .
Cho tam giác ABC nhọn không đều có trực tâm H nội tiếp trong đường tròn (O) sao cho tiếp tuyến của đường tròn (O) tại A cắt OH tại N. Gọi K là giao điểm hai tiếp tuyến của đường tròn (O) tại B và C, M là điểm đối xứng với A qua BC. Chứng minh K, M, N thẳng hàng.

Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Gọi M là một điểm trên cung nhỏ
B
C
⏜
(M khác B; C và AM không đi qua O). Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
1). Gọi D là điểm đối xứng với điểm M qua O. Chứng minh rằng ba điểm N, P, D thẳng hàng.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O) và ngoại tiếp đường tròn (I). Gọi M,N lần lượt là tiếp điểm của (I) với AC,AB. Đường trung bình song song với BC của tam giác ABC cắt (O) tại hai điểm P,Q. Chứng minh rằng M,N,P,Q cùng nằm trên một đường tròn.
Đề bài
Cho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng 12001200 ?
(A) (−−−→MN,−−→NP)(MN→,NP→);
(B) (−−→MO,−−→ON)(MO→,ON→);
(C) (−−−→MN,−−→OP)(MN→,OP→);
(D) (−−−→MN,−−→MP)(MN→,MP→).
Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:
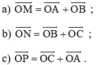
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.Gọi M là một điểm trên cung nhỏ
B
C
⏜
(M khác B; C và AM không đi qua O).Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O.
Gọi M là một điểm trên cung nhỏ B C ⏜ (M khác B; C và AM không đi qua O).
Giả sử P là một điểm thuộc đoạn thẳng AM sao cho đường tròn đường kính MP cắt cung nhỏ BC tại điểm N khác M.
2). Đường tròn đường kính MP cắt MD tại điểm Q khác M. Chứng minh rằng P là tâm đường tròn nội tiếp tam giác AQN.
Cho hình bình hành ABCD có
B
A
D
^
90
∘
. Giả sử O là điểm nằm trong
Δ
A
B
D
sao cho OC không vuông góc với BD. Vẽ đường tròn tâm O đi qua C. BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D. Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q1) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn.
Đọc tiếp
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C. BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
1) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn.
Cho tam giác không cân ABC. Gọi H, O lần lượt là trực tâm, tâm đường tròn ngoại tiếp của tam giác, M là trung điểm của cạnh BC. Khẳng định nào sau đây là đúng? A. Tam giác ABC nhọn thì
A
H
→
,
O
M
→
cùng hướng B.
A
H
→
,
O...
Đọc tiếp
Cho tam giác không cân ABC. Gọi H, O lần lượt là trực tâm, tâm đường tròn ngoại tiếp của tam giác, M là trung điểm của cạnh BC. Khẳng định nào sau đây là đúng?
A. Tam giác ABC nhọn thì A H → , O M → cùng hướng
B. A H → , O M → luôn cùng hướng
C. A H → , O M → cùng phương nhưng ngược hướng
D. A H → , O M → có cùng giá








